Cem Kalkanli
Batched Thompson Sampling
Oct 01, 2021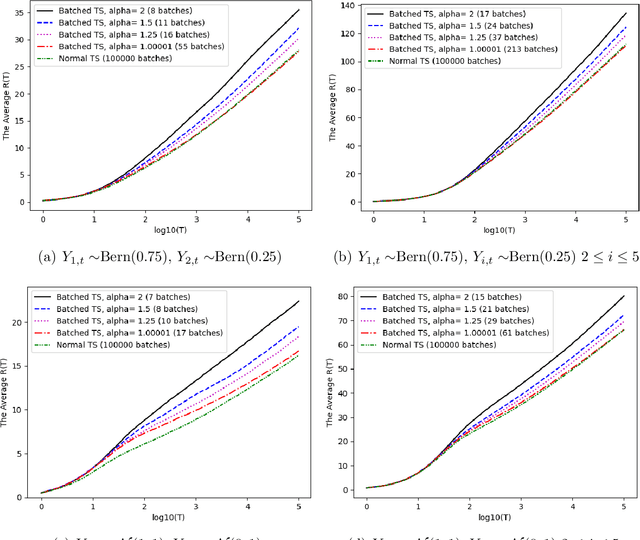
Abstract:We introduce a novel anytime Batched Thompson sampling policy for multi-armed bandits where the agent observes the rewards of her actions and adjusts her policy only at the end of a small number of batches. We show that this policy simultaneously achieves a problem dependent regret of order $O(\log(T))$ and a minimax regret of order $O(\sqrt{T\log(T)})$ while the number of batches can be bounded by $O(\log(T))$ independent of the problem instance over a time horizon $T$. We also show that in expectation the number of batches used by our policy can be bounded by an instance dependent bound of order $O(\log\log(T))$. These results indicate that Thompson sampling maintains the same performance in this batched setting as in the case when instantaneous feedback is available after each action, while requiring minimal feedback. These results also indicate that Thompson sampling performs competitively with recently proposed algorithms tailored for the batched setting. These algorithms optimize the batch structure for a given time horizon $T$ and prioritize exploration in the beginning of the experiment to eliminate suboptimal actions. We show that Thompson sampling combined with an adaptive batching strategy can achieve a similar performance without knowing the time horizon $T$ of the problem and without having to carefully optimize the batch structure to achieve a target regret bound (i.e. problem dependent vs minimax regret) for a given $T$.
Asymptotic Performance of Thompson Sampling in the Batched Multi-Armed Bandits
Oct 01, 2021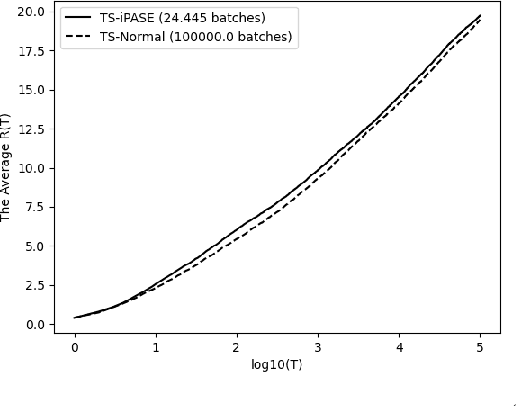
Abstract:We study the asymptotic performance of the Thompson sampling algorithm in the batched multi-armed bandit setting where the time horizon $T$ is divided into batches, and the agent is not able to observe the rewards of her actions until the end of each batch. We show that in this batched setting, Thompson sampling achieves the same asymptotic performance as in the case where instantaneous feedback is available after each action, provided that the batch sizes increase subexponentially. This result implies that Thompson sampling can maintain its performance even if it receives delayed feedback in $\omega(\log T)$ batches. We further propose an adaptive batching scheme that reduces the number of batches to $\Theta(\log T)$ while maintaining the same performance. Although the batched multi-armed bandit setting has been considered in several recent works, previous results rely on tailored algorithms for the batched setting, which optimize the batch structure and prioritize exploration in the beginning of the experiment to eliminate suboptimal actions. We show that Thompson sampling, on the other hand, is able to achieve a similar asymptotic performance in the batched setting without any modifications.
* This work was presented in 2021 IEEE International Symposium on Information Theory (ISIT)
Asymptotic Convergence of Thompson Sampling
Nov 08, 2020Abstract:Thompson sampling has been shown to be an effective policy across a variety of online learning tasks. Many works have analyzed the finite time performance of Thompson sampling, and proved that it achieves a sub-linear regret under a broad range of probabilistic settings. However its asymptotic behavior remains mostly underexplored. In this paper, we prove an asymptotic convergence result for Thompson sampling under the assumption of a sub-linear Bayesian regret, and show that the actions of a Thompson sampling agent provide a strongly consistent estimator of the optimal action. Our results rely on the martingale structure inherent in Thompson sampling.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge