One-Cold Poisson Channel: A Simple Continuous-Time Channel with Zero Dispersion

We introduce the one-cold Poisson channel (OCPC), where the transmitter chooses one of several frequency bands to attenuate at a time. In particular, the perfect OCPC, where the number of bands is unlimited, is an extremely simple continuous-time memoryless channel. It has a capacity 1, zero channel dispersion, and an information spectrum being the degenerate distribution at 1. It is the only known nontrivial (discrete or continuous-time) memoryless channel with a closed-form formula for its optimal non-asymptotic error probability, making it the simplest channel in this sense. A potential application is optical communication with a tunable band rejection filter. Due to its simplicity, we may use it as a basic currency of information that is infinitely divisible, as an alternative to bits which are not infinitely divisible. OCPC with perfect feedback gives a generalization of prefix codes. We also study non-asymptotic coding and channel simulation results for the general OCPC.

Communication-Efficient and Privacy-Adaptable Mechanism for Federated Learning

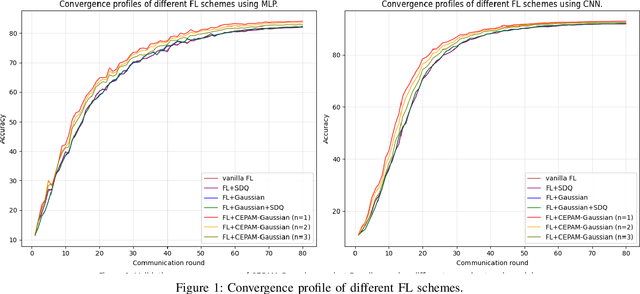
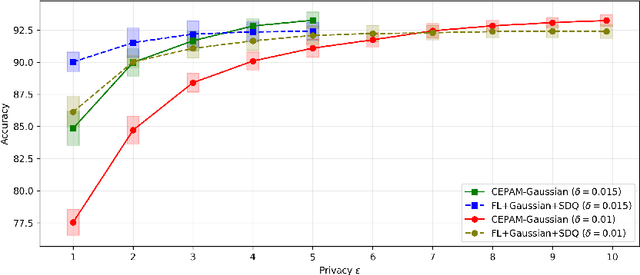
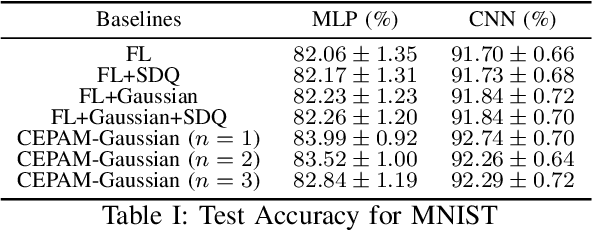
Training machine learning models on decentralized private data via federated learning (FL) poses two key challenges: communication efficiency and privacy protection. In this work, we address these challenges within the trusted aggregator model by introducing a novel approach called the Communication-Efficient and Privacy-Adaptable Mechanism (CEPAM), achieving both objectives simultaneously. In particular, CEPAM leverages the rejection-sampled universal quantizer (RSUQ), a construction of randomized vector quantizer whose resulting distortion is equivalent to a prescribed noise, such as Gaussian or Laplace noise, enabling joint differential privacy and compression. Moreover, we analyze the trade-offs among user privacy, global utility, and transmission rate of CEPAM by defining appropriate metrics for FL with differential privacy and compression. Our CEPAM provides the additional benefit of privacy adaptability, allowing clients and the server to customize privacy protection based on required accuracy and protection. We assess CEPAM's utility performance using MNIST dataset, demonstrating that CEPAM surpasses baseline models in terms of learning accuracy.

Be More Diverse than the Most Diverse: Online Selection of Diverse Mixtures of Generative Models

The availability of multiple training algorithms and architectures for generative models requires a selection mechanism to form a single model over a group of well-trained generation models. The selection task is commonly addressed by identifying the model that maximizes an evaluation score based on the diversity and quality of the generated data. However, such a best-model identification approach overlooks the possibility that a mixture of available models can outperform each individual model. In this work, we explore the selection of a mixture of multiple generative models and formulate a quadratic optimization problem to find an optimal mixture model achieving the maximum of kernel-based evaluation scores including kernel inception distance (KID) and R\'{e}nyi kernel entropy (RKE). To identify the optimal mixture of the models using the fewest possible sample queries, we propose an online learning approach called Mixture Upper Confidence Bound (Mixture-UCB). Specifically, our proposed online learning method can be extended to every convex quadratic function of the mixture weights, for which we prove a concentration bound to enable the application of the UCB approach. We prove a regret bound for the proposed Mixture-UCB algorithm and perform several numerical experiments to show the success of the proposed Mixture-UCB method in finding the optimal mixture of text-based and image-based generative models. The codebase is available at https://github.com/Rezaei-Parham/Mixture-UCB .

Universal Exact Compression of Differentially Private Mechanisms

To reduce the communication cost of differential privacy mechanisms, we introduce a novel construction, called Poisson private representation (PPR), designed to compress and simulate any local randomizer while ensuring local differential privacy. Unlike previous simulation-based local differential privacy mechanisms, PPR exactly preserves the joint distribution of the data and the output of the original local randomizer. Hence, the PPR-compressed privacy mechanism retains all desirable statistical properties of the original privacy mechanism such as unbiasedness and Gaussianity. Moreover, PPR achieves a compression size within a logarithmic gap from the theoretical lower bound. Using the PPR, we give a new order-wise trade-off between communication, accuracy, central and local differential privacy for distributed mean estimation. Experiment results on distributed mean estimation show that PPR consistently gives a better trade-off between communication, accuracy and central differential privacy compared to the coordinate subsampled Gaussian mechanism, while also providing local differential privacy.

Towards a Scalable Identification of Novel Modes in Generative Models

An interpretable comparison of generative models requires the identification of sample types produced more frequently by each of the involved models. While several quantitative scores have been proposed in the literature to rank different generative models, such score-based evaluations do not reveal the nuanced differences between the generative models in capturing various sample types. In this work, we propose a method called Fourier-based Identification of Novel Clusters (FINC) to identify modes produced by a generative model with a higher frequency in comparison to a reference distribution. FINC provides a scalable stochastic algorithm based on random Fourier features to estimate the eigenspace of kernel covariance matrices of two generative models and utilize the principal eigendirections to detect the sample types present more dominantly in each model. We demonstrate the application of the FINC method to standard computer vision datasets and generative model frameworks. Our numerical results suggest the scalability and efficiency of the developed Fourier-based method in highlighting the sample types captured with different frequencies by widely-used generative models.

An Interpretable Evaluation of Entropy-based Novelty of Generative Models

The massive developments of generative model frameworks and architectures require principled methods for the evaluation of a model's novelty compared to a reference dataset or baseline generative models. While the recent literature has extensively studied the evaluation of the quality, diversity, and generalizability of generative models, the assessment of a model's novelty compared to a baseline model has not been adequately studied in the machine learning community. In this work, we focus on the novelty assessment under multi-modal generative models and attempt to answer the following question: Given the samples of a generative model $\mathcal{G}$ and a reference dataset $\mathcal{S}$, how can we discover and count the modes expressed by $\mathcal{G}$ more frequently than in $\mathcal{S}$. We introduce a spectral approach to the described task and propose the Kernel-based Entropic Novelty (KEN) score to quantify the mode-based novelty of distribution $P_\mathcal{G}$ with respect to distribution $P_\mathcal{S}$. We analytically interpret the behavior of the KEN score under mixture distributions with sub-Gaussian components. Next, we develop a method based on Cholesky decomposition to compute the KEN score from observed samples. We support the KEN-based quantification of novelty by presenting several numerical results on synthetic and real image distributions. Our numerical results indicate the success of the proposed approach in detecting the novel modes and the comparison of state-of-the-art generative models.

Rejection-Sampled Universal Quantization for Smaller Quantization Errors

We construct a randomized vector quantizer which has a smaller maximum error compared to all known lattice quantizers with the same entropy for dimensions 5, 6, ..., 48, and also has a smaller mean squared error compared to known lattice quantizers with the same entropy for dimensions 35, ..., 48, in the high resolution limit. Moreover, our randomized quantizer has a desirable property that the quantization error is always uniform over the ball and independent of the input. Our construction is based on applying rejection sampling on universal quantization, which allows us to shape the error distribution to be any continuous distribution, not only uniform distributions over basic cells of a lattice as in conventional dithered quantization. We also characterize the high SNR limit of one-shot channel simulation for any additive noise channel under a mild assumption (e.g., the AWGN channel), up to an additive constant of 1.45 bits.

Compression with Exact Error Distribution for Federated Learning

Compression schemes have been extensively used in Federated Learning (FL) to reduce the communication cost of distributed learning. While most approaches rely on a bounded variance assumption of the noise produced by the compressor, this paper investigates the use of compression and aggregation schemes that produce a specific error distribution, e.g., Gaussian or Laplace, on the aggregated data. We present and analyze different aggregation schemes based on layered quantizers achieving exact error distribution. We provide different methods to leverage the proposed compression schemes to obtain compression-for-free in differential privacy applications. Our general compression methods can recover and improve standard FL schemes with Gaussian perturbations such as Langevin dynamics and randomized smoothing.

Locally Weighted Learning for Naive Bayes Classifier

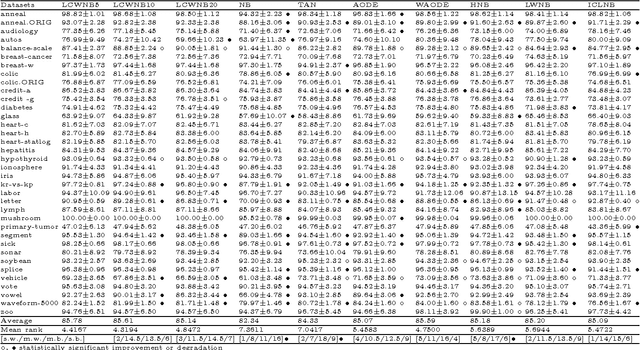
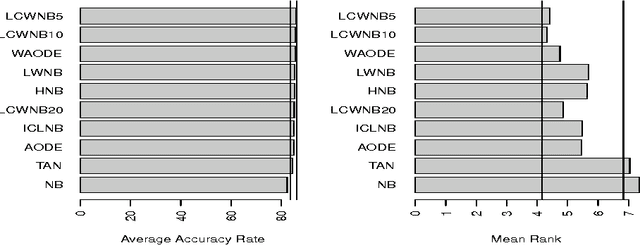
As a consequence of the strong and usually violated conditional independence assumption (CIA) of naive Bayes (NB) classifier, the performance of NB becomes less and less favorable compared to sophisticated classifiers when the sample size increases. We learn from this phenomenon that when the size of the training data is large, we should either relax the assumption or apply NB to a "reduced" data set, say for example use NB as a local model. The latter approach trades the ignored information for the robustness to the model assumption. In this paper, we consider using NB as a model for locally weighted data. A special weighting function is designed so that if CIA holds for the unweighted data, it also holds for the weighted data. The new method is intuitive and capable of handling class imbalance. It is theoretically more sound than the locally weighted learners of naive Bayes that base classification only on the $k$ nearest neighbors. Empirical study shows that the new method with appropriate choice of parameter outperforms seven existing classifiers of similar nature.