The Maximum von Neumann Entropy Principle: Theory and Applications in Machine Learning

Von Neumann entropy (VNE) is a fundamental quantity in quantum information theory and has recently been adopted in machine learning as a spectral measure of diversity for kernel matrices and kernel covariance operators. While maximizing VNE under constraints is well known in quantum settings, a principled analogue of the classical maximum entropy framework, particularly its decision theoretic and game theoretic interpretation, has not been explicitly developed for VNE in data driven contexts. In this paper, we extend the minimax formulation of the maximum entropy principle due to Grünwald and Dawid to the setting of von Neumann entropy, providing a game-theoretic justification for VNE maximization over density matrices and trace-normalized positive semidefinite operators. This perspective yields a robust interpretation of maximum VNE solutions under partial information and clarifies their role as least committed inferences in spectral domains. We then illustrate how the resulting Maximum VNE principle applies to modern machine learning problems by considering two representative applications, selecting a kernel representation from multiple normalized embeddings via kernel-based VNE maximization, and completing kernel matrices from partially observed entries. These examples demonstrate how the proposed framework offers a unifying information-theoretic foundation for VNE-based methods in kernel learning.

Fusing Cross-modal and Uni-modal Representations: A Kronecker Product Approach

Cross-modal embeddings, such as CLIP, BLIP and their variants, have achieved promising results in aligning representations across modalities. However, these embeddings could underperform compared to state-of-the-art single-modality embeddings on modality-specific tasks. On the other hand, single-modality embeddings excel in their domains but lack cross-modal alignment capabilities. In this work, we focus on the problem of unifying cross-modality and single-modality embeddings to achieve the performance of modality-expert embedding within individual modalities while preserving cross-modal alignment. To this end, we propose RP-KrossFuse, a method that leverages a random projection-based Kronecker product to integrate cross-modal embeddings with single-modality embeddings. RP-KrossFuse aims to fuse the sample-pairwise similarity scores of the fused embeddings and operates efficiently in a specified kernel space and supports scalable implementations via random Fourier features for shift-invariant kernels such as the Gaussian kernel. We demonstrate the effectiveness of RP-KrossFuse through several numerical experiments, combining CLIP embeddings with uni-modal image and text embeddings. Our numerical results indicate that RP-KrossFuse achieves competitive modality-specific performance while retaining cross-modal alignment, bridging the gap between cross-modal and single-modality embeddings.

Communication-Efficient and Privacy-Adaptable Mechanism for Federated Learning

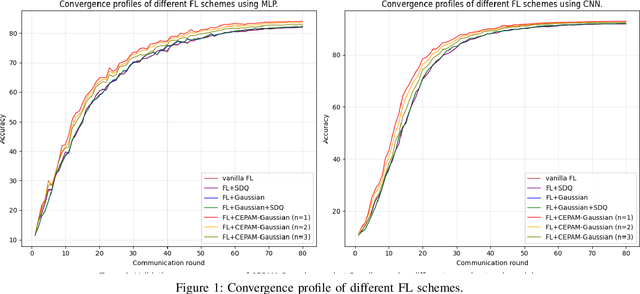
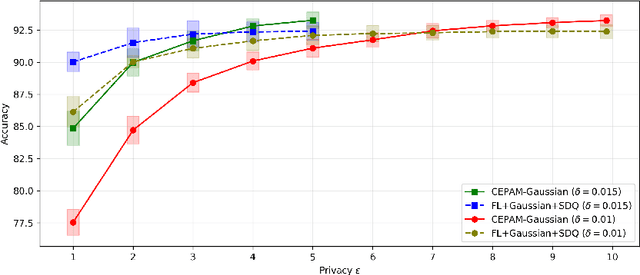
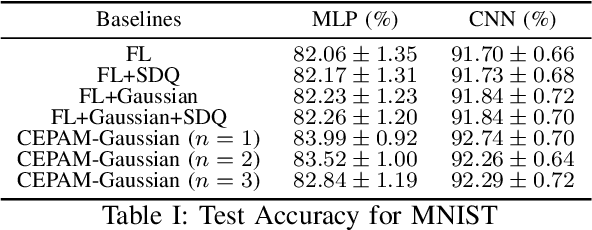
Training machine learning models on decentralized private data via federated learning (FL) poses two key challenges: communication efficiency and privacy protection. In this work, we address these challenges within the trusted aggregator model by introducing a novel approach called the Communication-Efficient and Privacy-Adaptable Mechanism (CEPAM), achieving both objectives simultaneously. In particular, CEPAM leverages the rejection-sampled universal quantizer (RSUQ), a construction of randomized vector quantizer whose resulting distortion is equivalent to a prescribed noise, such as Gaussian or Laplace noise, enabling joint differential privacy and compression. Moreover, we analyze the trade-offs among user privacy, global utility, and transmission rate of CEPAM by defining appropriate metrics for FL with differential privacy and compression. Our CEPAM provides the additional benefit of privacy adaptability, allowing clients and the server to customize privacy protection based on required accuracy and protection. We assess CEPAM's utility performance using MNIST dataset, demonstrating that CEPAM surpasses baseline models in terms of learning accuracy.