PromptSplit: Revealing Prompt-Level Disagreement in Generative Models

Prompt-guided generative AI models have rapidly expanded across vision and language domains, producing realistic and diverse outputs from textual inputs. The growing variety of such models, trained with different data and architectures, calls for principled methods to identify which types of prompts lead to distinct model behaviors. In this work, we propose PromptSplit, a kernel-based framework for detecting and analyzing prompt-dependent disagreement between generative models. For each compared model pair, PromptSplit constructs a joint prompt--output representation by forming tensor-product embeddings of the prompt and image (or text) features, and then computes the corresponding kernel covariance matrix. We utilize the eigenspace of the weighted difference between these matrices to identify the main directions of behavioral difference across prompts. To ensure scalability, we employ a random-projection approximation that reduces computational complexity to $O(nr^2 + r^3)$ for projection dimension $r$. We further provide a theoretical analysis showing that this approximation yields an eigenstructure estimate whose expected deviation from the full-dimensional result is bounded by $O(1/r^2)$. Experiments across text-to-image, text-to-text, and image-captioning settings demonstrate that PromptSplit accurately detects ground-truth behavioral differences and isolates the prompts responsible, offering an interpretable tool for detecting where generative models disagree.

On the Fragility of AI-Based Channel Decoders under Small Channel Perturbations

Recent advances in deep learning have led to AI-based error correction decoders that report empirical performance improvements over traditional belief-propagation (BP) decoding on AWGN channels. While such gains are promising, a fundamental question remains: where do these improvements come from, and what cost is paid to achieve them? In this work, we study this question through the lens of robustness to distributional shifts at the channel output. We evaluate both input-dependent adversarial perturbations (FGM and projected gradient methods under $\ell_2$ constraints) and universal adversarial perturbations that apply a single norm-bounded shift to all received vectors. Our results show that recent AI decoders, including ECCT and CrossMPT, could suffer significant performance degradation under such perturbations, despite superior nominal performance under i.i.d. AWGN. Moreover, adversarial perturbations transfer relatively strongly between AI decoders but weakly to BP-based decoders, and universal perturbations are substantially more harmful than random perturbations of equal norm. These numerical findings suggest a potential robustness cost and higher sensitivity to channel distribution underlying recent AI decoding gains.

Training-Free Distribution Adaptation for Diffusion Models via Maximum Mean Discrepancy Guidance

Pre-trained diffusion models have emerged as powerful generative priors for both unconditional and conditional sample generation, yet their outputs often deviate from the characteristics of user-specific target data. Such mismatches are especially problematic in domain adaptation tasks, where only a few reference examples are available and retraining the diffusion model is infeasible. Existing inference-time guidance methods can adjust sampling trajectories, but they typically optimize surrogate objectives such as classifier likelihoods rather than directly aligning with the target distribution. We propose MMD Guidance, a training-free mechanism that augments the reverse diffusion process with gradients of the Maximum Mean Discrepancy (MMD) between generated samples and a reference dataset. MMD provides reliable distributional estimates from limited data, exhibits low variance in practice, and is efficiently differentiable, which makes it particularly well-suited for the guidance task. Our framework naturally extends to prompt-aware adaptation in conditional generation models via product kernels. Also, it can be applied with computational efficiency in latent diffusion models (LDMs), since guidance is applied in the latent space of the LDM. Experiments on synthetic and real-world benchmarks demonstrate that MMD Guidance can achieve distributional alignment while preserving sample fidelity.

SPARKE: Scalable Prompt-Aware Diversity Guidance in Diffusion Models via RKE Score

Diffusion models have demonstrated remarkable success in high-fidelity image synthesis and prompt-guided generative modeling. However, ensuring adequate diversity in generated samples of prompt-guided diffusion models remains a challenge, particularly when the prompts span a broad semantic spectrum and the diversity of generated data needs to be evaluated in a prompt-aware fashion across semantically similar prompts. Recent methods have introduced guidance via diversity measures to encourage more varied generations. In this work, we extend the diversity measure-based approaches by proposing the Scalable Prompt-Aware R\'eny Kernel Entropy Diversity Guidance (SPARKE) method for prompt-aware diversity guidance. SPARKE utilizes conditional entropy for diversity guidance, which dynamically conditions diversity measurement on similar prompts and enables prompt-aware diversity control. While the entropy-based guidance approach enhances prompt-aware diversity, its reliance on the matrix-based entropy scores poses computational challenges in large-scale generation settings. To address this, we focus on the special case of Conditional latent RKE Score Guidance, reducing entropy computation and gradient-based optimization complexity from the $O(n^3)$ of general entropy measures to $O(n)$. The reduced computational complexity allows for diversity-guided sampling over potentially thousands of generation rounds on different prompts. We numerically test the SPARKE method on several text-to-image diffusion models, demonstrating that the proposed method improves the prompt-aware diversity of the generated data without incurring significant computational costs. We release our code on the project page: https://mjalali.github.io/SPARKE

Towards an Explainable Comparison and Alignment of Feature Embeddings

While several feature embedding models have been developed in the literature, comparisons of these embeddings have largely focused on their numerical performance in classification-related downstream applications. However, an interpretable comparison of different embeddings requires identifying and analyzing mismatches between sample groups clustered within the embedding spaces. In this work, we propose the \emph{Spectral Pairwise Embedding Comparison (SPEC)} framework to compare embeddings and identify their differences in clustering a reference dataset. Our approach examines the kernel matrices derived from two embeddings and leverages the eigendecomposition of the difference kernel matrix to detect sample clusters that are captured differently by the two embeddings. We present a scalable implementation of this kernel-based approach, with computational complexity that grows linearly with the sample size. Furthermore, we introduce an optimization problem using this framework to align two embeddings, ensuring that clusters identified in one embedding are also captured in the other model. We provide numerical results demonstrating the SPEC's application to compare and align embeddings on large-scale datasets such as ImageNet and MS-COCO. The code is available at [https://github.com/mjalali/embedding-comparison](github.com/mjalali/embedding-comparison).

Dissecting CLIP: Decomposition with a Schur Complement-based Approach

The use of CLIP embeddings to assess the alignment of samples produced by text-to-image generative models has been extensively explored in the literature. While the widely adopted CLIPScore, derived from the cosine similarity of text and image embeddings, effectively measures the relevance of a generated image, it does not quantify the diversity of images generated by a text-to-image model. In this work, we extend the application of CLIP embeddings to quantify and interpret the intrinsic diversity of text-to-image models, which is responsible for generating diverse images from similar text prompts. To achieve this, we propose a decomposition of the CLIP-based kernel covariance matrix of image data into text-based and non-text-based components. Using the Schur complement of the joint image-text kernel covariance matrix, we perform this decomposition and define the matrix-based entropy of the decomposed component as the \textit{Schur Complement Entropy (SCE)} score, a measure of the intrinsic diversity of a text-to-image model based on data collected with varying text prompts. Additionally, we demonstrate the use of the Schur complement-based decomposition to nullify the influence of a given prompt in the CLIP embedding of an image, enabling focus or defocus of embeddings on specific objects or properties for downstream tasks. We present several numerical results that apply our Schur complement-based approach to evaluate text-to-image models and modify CLIP image embeddings. The codebase is available at https://github.com/aziksh-ospanov/CLIP-DISSECTION

Conditional Vendi Score: An Information-Theoretic Approach to Diversity Evaluation of Prompt-based Generative Models

Text-conditioned generation models are commonly evaluated based on the quality of the generated data and its alignment with the input text prompt. On the other hand, several applications of prompt-based generative models require sufficient diversity in the generated data to ensure the models' capability of generating image and video samples possessing a variety of features. However, most existing diversity metrics are designed for unconditional generative models, and thus cannot distinguish the diversity arising from variations in text prompts and that contributed by the generative model itself. In this work, our goal is to quantify the prompt-induced and model-induced diversity in samples generated by prompt-based models. We propose an information-theoretic approach for internal diversity quantification, where we decompose the kernel-based entropy $H(X)$ of the generated data $X$ into the sum of the conditional entropy $H(X|T)$, given text variable $T$, and the mutual information $I(X; T)$ between the text and data variables. We introduce the \emph{Conditional-Vendi} score based on $H(X|T)$ to quantify the internal diversity of the model and the \emph{Information-Vendi} score based on $I(X; T)$ to measure the statistical relevance between the generated data and text prompts. We provide theoretical results to statistically interpret these scores and relate them to the unconditional Vendi score. We conduct several numerical experiments to show the correlation between the Conditional-Vendi score and the internal diversity of text-conditioned generative models. The codebase is available at \href{https://github.com/mjalali/conditional-vendi}{https://github.com/mjalali/conditional-vendi}.

Towards a Scalable Reference-Free Evaluation of Generative Models

While standard evaluation scores for generative models are mostly reference-based, a reference-dependent assessment of generative models could be generally difficult due to the unavailability of applicable reference datasets. Recently, the reference-free entropy scores, VENDI and RKE, have been proposed to evaluate the diversity of generated data. However, estimating these scores from data leads to significant computational costs for large-scale generative models. In this work, we leverage the random Fourier features framework to reduce the computational price and propose the Fourier-based Kernel Entropy Approximation (FKEA) method. We utilize FKEA's approximated eigenspectrum of the kernel matrix to efficiently estimate the mentioned entropy scores. Furthermore, we show the application of FKEA's proxy eigenvectors to reveal the method's identified modes in evaluating the diversity of produced samples. We provide a stochastic implementation of the FKEA assessment algorithm with a complexity $O(n)$ linearly growing with sample size $n$. We extensively evaluate FKEA's numerical performance in application to standard image, text, and video datasets. Our empirical results indicate the method's scalability and interpretability applied to large-scale generative models. The codebase is available at https://github.com/aziksh-ospanov/FKEA.

Towards a Scalable Identification of Novel Modes in Generative Models

An interpretable comparison of generative models requires the identification of sample types produced more frequently by each of the involved models. While several quantitative scores have been proposed in the literature to rank different generative models, such score-based evaluations do not reveal the nuanced differences between the generative models in capturing various sample types. In this work, we propose a method called Fourier-based Identification of Novel Clusters (FINC) to identify modes produced by a generative model with a higher frequency in comparison to a reference distribution. FINC provides a scalable stochastic algorithm based on random Fourier features to estimate the eigenspace of kernel covariance matrices of two generative models and utilize the principal eigendirections to detect the sample types present more dominantly in each model. We demonstrate the application of the FINC method to standard computer vision datasets and generative model frameworks. Our numerical results suggest the scalability and efficiency of the developed Fourier-based method in highlighting the sample types captured with different frequencies by widely-used generative models.

Game of GANs: Game Theoretical Models for Generative Adversarial Networks

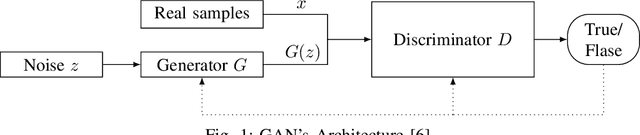
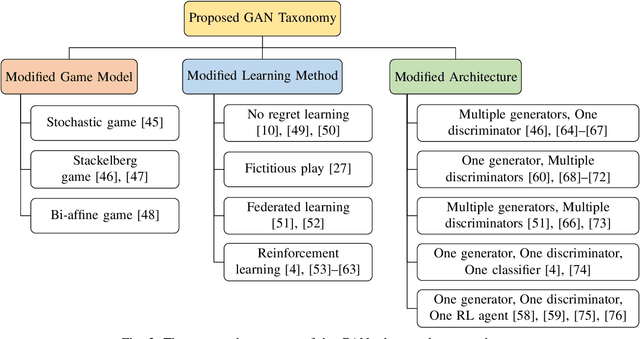
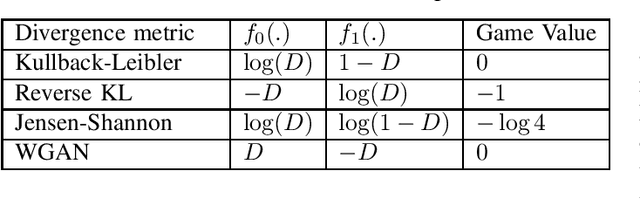
Generative Adversarial Network, as a promising research direction in the AI community, recently attracts considerable attention due to its ability to generating high-quality realistic data. GANs are a competing game between two neural networks trained in an adversarial manner to reach a Nash equilibrium. Despite the improvement accomplished in GANs in the last years, there remain several issues to solve. In this way, how to tackle these issues and make advances leads to rising research interests. This paper reviews literature that leverages the game theory in GANs and addresses how game models can relieve specific generative models' challenges and improve the GAN's performance. In particular, we firstly review some preliminaries, including the basic GAN model and some game theory backgrounds. After that, we present our taxonomy to summarize the state-of-the-art solutions into three significant categories: modified game model, modified architecture, and modified learning method. The classification is based on the modifications made in the basic model by the proposed approaches from the game-theoretic perspective. We further classify each category into several subcategories. Following the proposed taxonomy, we explore the main objective of each class and review the recent work in each group. Finally, we discuss the remaining challenges in this field and present the potential future research topics.