Towards a Scalable Reference-Free Evaluation of Generative Models

While standard evaluation scores for generative models are mostly reference-based, a reference-dependent assessment of generative models could be generally difficult due to the unavailability of applicable reference datasets. Recently, the reference-free entropy scores, VENDI and RKE, have been proposed to evaluate the diversity of generated data. However, estimating these scores from data leads to significant computational costs for large-scale generative models. In this work, we leverage the random Fourier features framework to reduce the computational price and propose the Fourier-based Kernel Entropy Approximation (FKEA) method. We utilize FKEA's approximated eigenspectrum of the kernel matrix to efficiently estimate the mentioned entropy scores. Furthermore, we show the application of FKEA's proxy eigenvectors to reveal the method's identified modes in evaluating the diversity of produced samples. We provide a stochastic implementation of the FKEA assessment algorithm with a complexity $O(n)$ linearly growing with sample size $n$. We extensively evaluate FKEA's numerical performance in application to standard image, text, and video datasets. Our empirical results indicate the method's scalability and interpretability applied to large-scale generative models. The codebase is available at https://github.com/aziksh-ospanov/FKEA.

Learning and Testing Variable Partitions

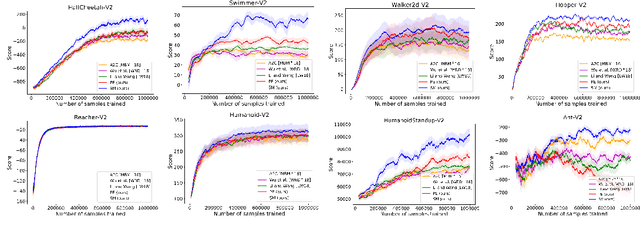
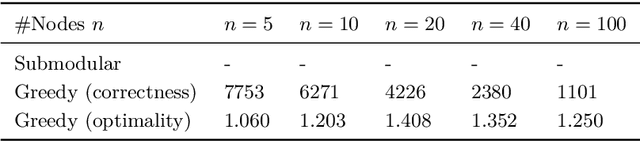
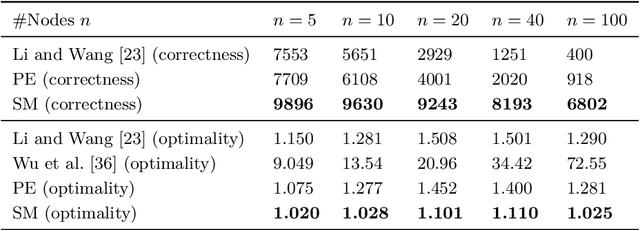
$ $Let $F$ be a multivariate function from a product set $\Sigma^n$ to an Abelian group $G$. A $k$-partition of $F$ with cost $\delta$ is a partition of the set of variables $\mathbf{V}$ into $k$ non-empty subsets $(\mathbf{X}_1, \dots, \mathbf{X}_k)$ such that $F(\mathbf{V})$ is $\delta$-close to $F_1(\mathbf{X}_1)+\dots+F_k(\mathbf{X}_k)$ for some $F_1, \dots, F_k$ with respect to a given error metric. We study algorithms for agnostically learning $k$ partitions and testing $k$-partitionability over various groups and error metrics given query access to $F$. In particular we show that $1.$ Given a function that has a $k$-partition of cost $\delta$, a partition of cost $\mathcal{O}(k n^2)(\delta + \epsilon)$ can be learned in time $\tilde{\mathcal{O}}(n^2 \mathrm{poly} (1/\epsilon))$ for any $\epsilon > 0$. In contrast, for $k = 2$ and $n = 3$ learning a partition of cost $\delta + \epsilon$ is NP-hard. $2.$ When $F$ is real-valued and the error metric is the 2-norm, a 2-partition of cost $\sqrt{\delta^2 + \epsilon}$ can be learned in time $\tilde{\mathcal{O}}(n^5/\epsilon^2)$. $3.$ When $F$ is $\mathbb{Z}_q$-valued and the error metric is Hamming weight, $k$-partitionability is testable with one-sided error and $\mathcal{O}(kn^3/\epsilon)$ non-adaptive queries. We also show that even two-sided testers require $\Omega(n)$ queries when $k = 2$. This work was motivated by reinforcement learning control tasks in which the set of control variables can be partitioned. The partitioning reduces the task into multiple lower-dimensional ones that are relatively easier to learn. Our second algorithm empirically increases the scores attained over previous heuristic partitioning methods applied in this context.