Learning and Testing Variable Partitions
Paper and Code
Mar 29, 2020
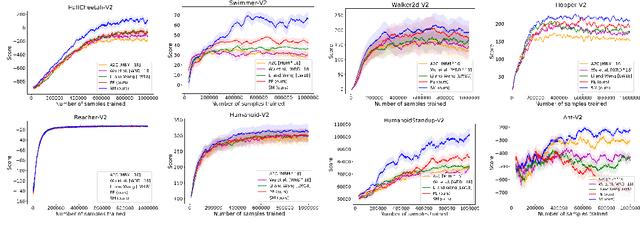
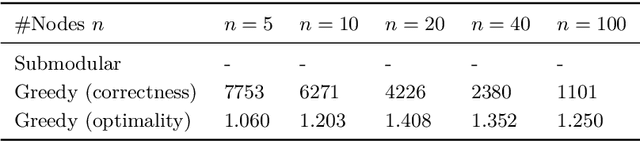
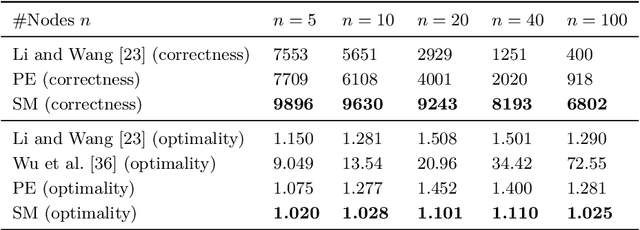
$ $Let $F$ be a multivariate function from a product set $\Sigma^n$ to an Abelian group $G$. A $k$-partition of $F$ with cost $\delta$ is a partition of the set of variables $\mathbf{V}$ into $k$ non-empty subsets $(\mathbf{X}_1, \dots, \mathbf{X}_k)$ such that $F(\mathbf{V})$ is $\delta$-close to $F_1(\mathbf{X}_1)+\dots+F_k(\mathbf{X}_k)$ for some $F_1, \dots, F_k$ with respect to a given error metric. We study algorithms for agnostically learning $k$ partitions and testing $k$-partitionability over various groups and error metrics given query access to $F$. In particular we show that $1.$ Given a function that has a $k$-partition of cost $\delta$, a partition of cost $\mathcal{O}(k n^2)(\delta + \epsilon)$ can be learned in time $\tilde{\mathcal{O}}(n^2 \mathrm{poly} (1/\epsilon))$ for any $\epsilon > 0$. In contrast, for $k = 2$ and $n = 3$ learning a partition of cost $\delta + \epsilon$ is NP-hard. $2.$ When $F$ is real-valued and the error metric is the 2-norm, a 2-partition of cost $\sqrt{\delta^2 + \epsilon}$ can be learned in time $\tilde{\mathcal{O}}(n^5/\epsilon^2)$. $3.$ When $F$ is $\mathbb{Z}_q$-valued and the error metric is Hamming weight, $k$-partitionability is testable with one-sided error and $\mathcal{O}(kn^3/\epsilon)$ non-adaptive queries. We also show that even two-sided testers require $\Omega(n)$ queries when $k = 2$. This work was motivated by reinforcement learning control tasks in which the set of control variables can be partitioned. The partitioning reduces the task into multiple lower-dimensional ones that are relatively easier to learn. Our second algorithm empirically increases the scores attained over previous heuristic partitioning methods applied in this context.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge