Optimal Compression of Locally Differentially Private Mechanisms
Paper and Code
Oct 29, 2021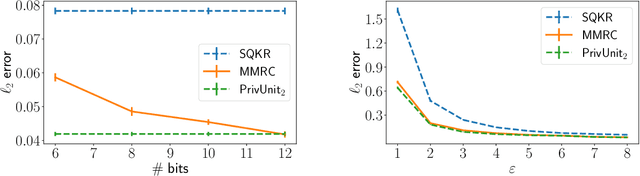
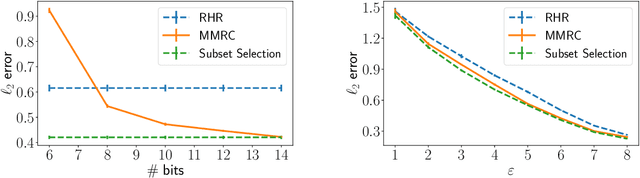
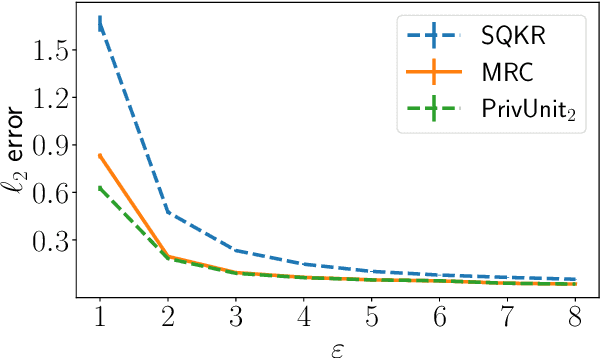
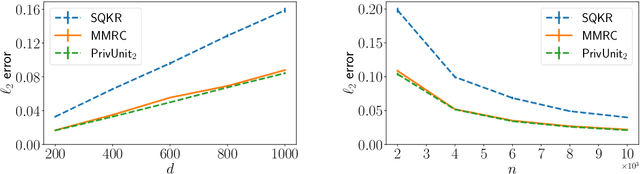
Compressing the output of \epsilon-locally differentially private (LDP) randomizers naively leads to suboptimal utility. In this work, we demonstrate the benefits of using schemes that jointly compress and privatize the data using shared randomness. In particular, we investigate a family of schemes based on Minimal Random Coding (Havasi et al., 2019) and prove that they offer optimal privacy-accuracy-communication tradeoffs. Our theoretical and empirical findings show that our approach can compress PrivUnit (Bhowmick et al., 2018) and Subset Selection (Ye et al., 2018), the best known LDP algorithms for mean and frequency estimation, to to the order of \epsilon-bits of communication while preserving their privacy and accuracy guarantees.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge