Finding Valid Adjustments under Non-ignorability with Minimal DAG Knowledge

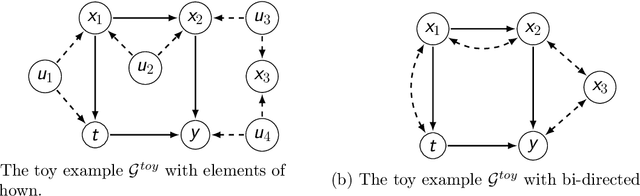
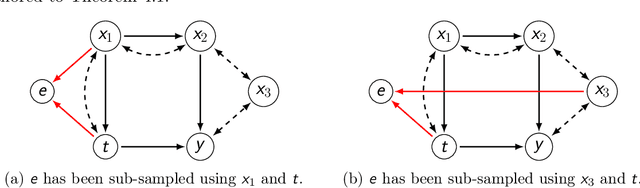
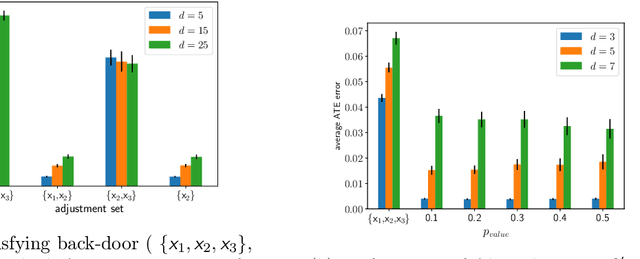
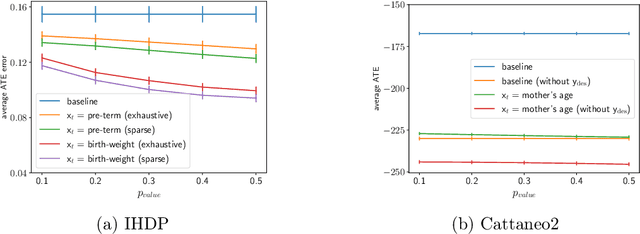
Treatment effect estimation from observational data is a fundamental problem in causal inference. There are two very different schools of thought that have tackled this problem. On the one hand, the Pearlian framework commonly assumes structural knowledge (provided by an expert) in the form of Directed Acyclic Graphs (DAGs) and provides graphical criteria such as the back-door criterion to identify the valid adjustment sets. On the other hand, the potential outcomes (PO) framework commonly assumes that all the observed features satisfy ignorability (i.e., no hidden confounding), which in general is untestable. In this work, we take steps to bridge these two frameworks. We show that even if we know only one parent of the treatment variable (provided by an expert), then quite remarkably it suffices to test a broad class of (but not all) back-door criteria. Importantly, we also cover the non-trivial case where the entire set of observed features is not ignorable (generalizing the PO framework) without requiring all the parents of the treatment variable to be observed. Our key technical idea involves a more general result -- Given a synthetic sub-sampling (or environment) variable that is a function of the parent variable, we show that an invariance test involving this sub-sampling variable is equivalent to testing a broad class of back-door criteria. We demonstrate our approach on synthetic data as well as real causal effect estimation benchmarks.