Selective Regression Under Fairness Criteria
Paper and Code
Oct 28, 2021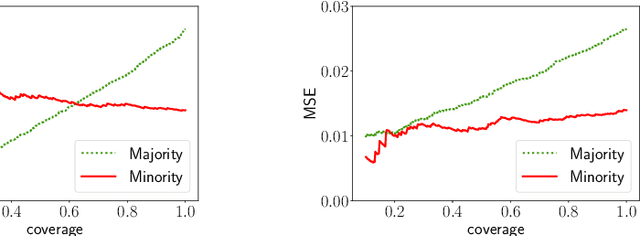
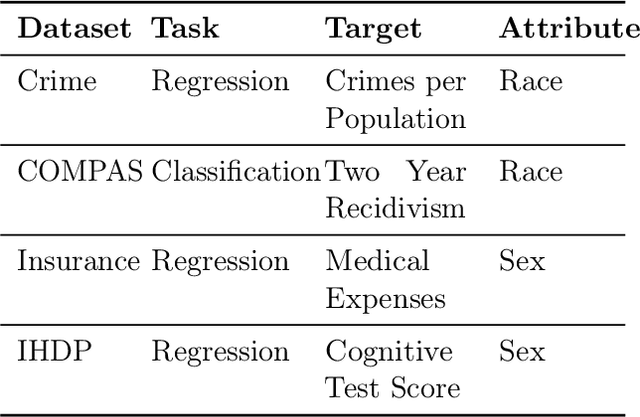
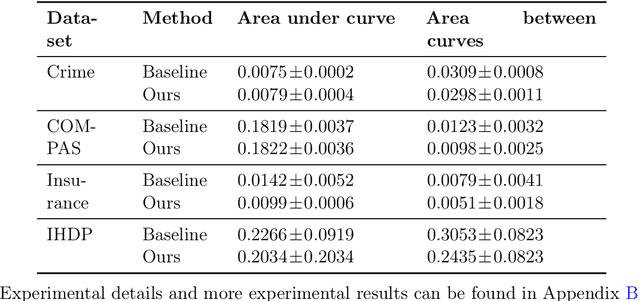
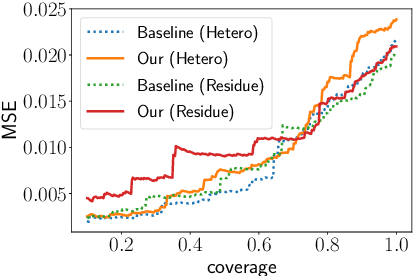
Selective regression allows abstention from prediction if the confidence to make an accurate prediction is not sufficient. In general, by allowing a reject option, one expects the performance of a regression model to increase at the cost of reducing coverage (i.e., by predicting fewer samples). However, as shown in this work, in some cases, the performance of minority group can decrease while we reduce the coverage, and thus selective regression can magnify disparities between different sensitive groups. We show that such an unwanted behavior can be avoided if we can construct features satisfying the sufficiency criterion, so that the mean prediction and the associated uncertainty are calibrated across all the groups. Further, to mitigate the disparity in the performance across groups, we introduce two approaches based on this calibration criterion: (a) by regularizing an upper bound of conditional mutual information under a Gaussian assumption and (b) by regularizing a contrastive loss for mean and uncertainty prediction. The effectiveness of these approaches are demonstrated on synthetic as well as real-world datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge