Doubly Robust Inference in Causal Latent Factor Models
Paper and Code
Feb 18, 2024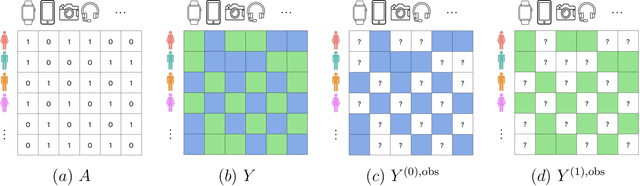
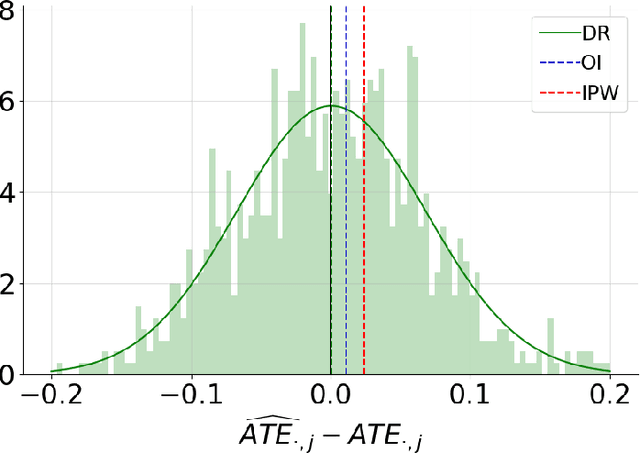
This article introduces a new framework for estimating average treatment effects under unobserved confounding in modern data-rich environments featuring large numbers of units and outcomes. The proposed estimator is doubly robust, combining outcome imputation, inverse probability weighting, and a novel cross-fitting procedure for matrix completion. We derive finite-sample and asymptotic guarantees, and show that the error of the new estimator converges to a mean-zero Gaussian distribution at a parametric rate. Simulation results demonstrate the practical relevance of the formal properties of the estimators analyzed in this article.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge