Entry-Specific Matrix Estimation under Arbitrary Sampling Patterns through the Lens of Network Flows

Matrix completion tackles the task of predicting missing values in a low-rank matrix based on a sparse set of observed entries. It is often assumed that the observation pattern is generated uniformly at random or has a very specific structure tuned to a given algorithm. There is still a gap in our understanding when it comes to arbitrary sampling patterns. Given an arbitrary sampling pattern, we introduce a matrix completion algorithm based on network flows in the bipartite graph induced by the observation pattern. For additive matrices, the particular flow we used is the electrical flow and we establish error upper bounds customized to each entry as a function of the observation set, along with matching minimax lower bounds. Our results show that the minimax squared error for recovery of a particular entry in the matrix is proportional to the effective resistance of the corresponding edge in the graph. Furthermore, we show that our estimator is equivalent to the least squares estimator. We apply our estimator to the two-way fixed effects model and show that it enables us to accurately infer individual causal effects and the unit-specific and time-specific confounders. For rank-$1$ matrices, we use edge-disjoint paths to form an estimator that achieves minimax optimal estimation when the sampling is sufficiently dense. Our discovery introduces a new family of estimators parametrized by network flows, which provide a fine-grained and intuitive understanding of the impact of the given sampling pattern on the relative difficulty of estimation at an entry-specific level. This graph-based approach allows us to quantify the inherent complexity of matrix completion for individual entries, rather than relying solely on global measures of performance.

Entry-Specific Bounds for Low-Rank Matrix Completion under Highly Non-Uniform Sampling

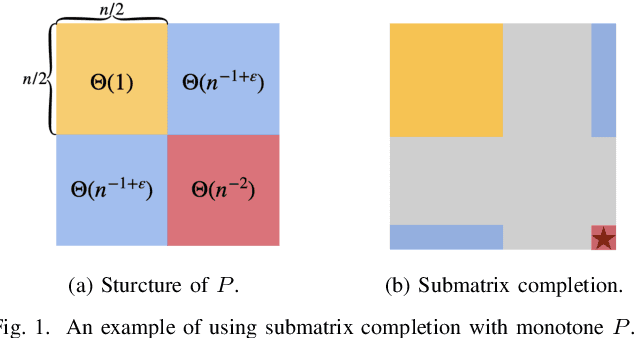
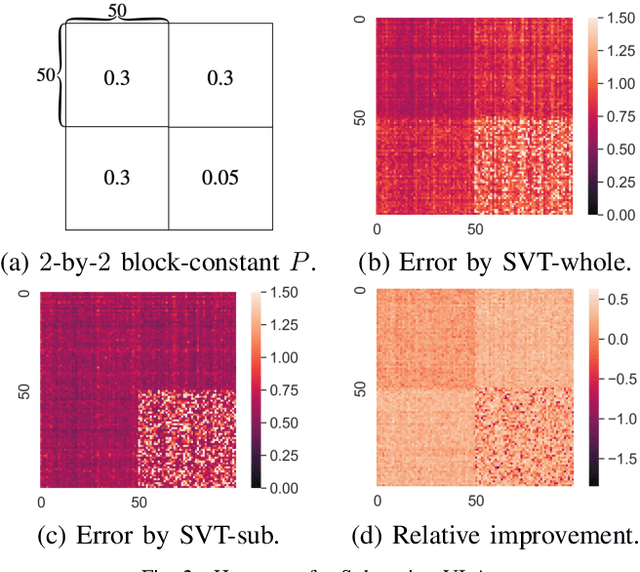
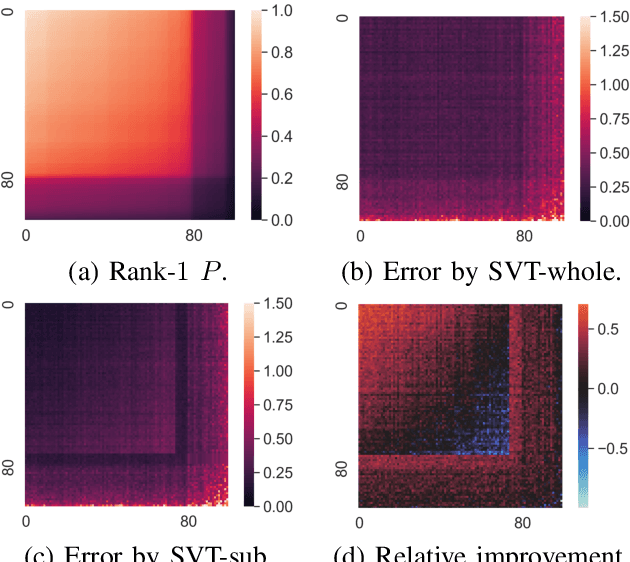
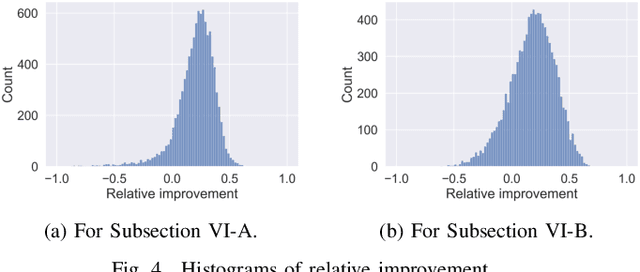
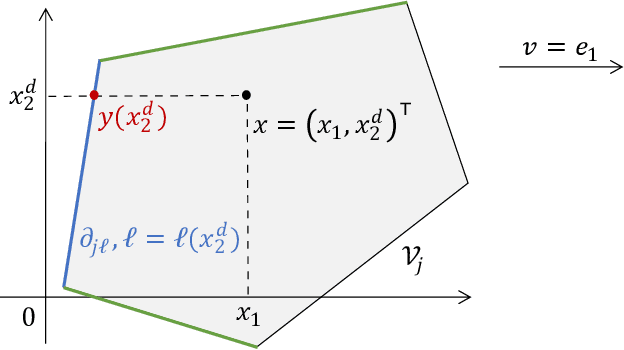
Low-rank matrix completion concerns the problem of estimating unobserved entries in a matrix using a sparse set of observed entries. We consider the non-uniform setting where the observed entries are sampled with highly varying probabilities, potentially with different asymptotic scalings. We show that under structured sampling probabilities, it is often better and sometimes optimal to run estimation algorithms on a smaller submatrix rather than the entire matrix. In particular, we prove error upper bounds customized to each entry, which match the minimax lower bounds under certain conditions. Our bounds characterize the hardness of estimating each entry as a function of the localized sampling probabilities. We provide numerical experiments that confirm our theoretical findings.

Integrating Offline Reinforcement Learning with Transformers for Sequential Recommendation

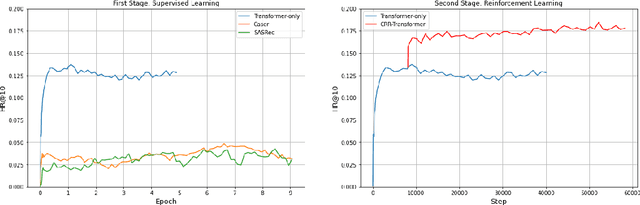
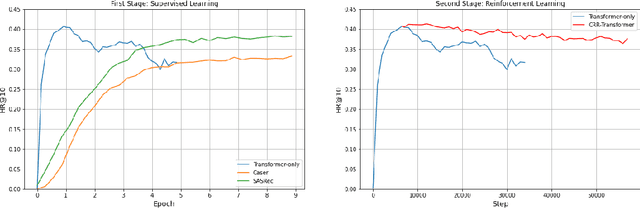
We consider the problem of sequential recommendation, where the current recommendation is made based on past interactions. This recommendation task requires efficient processing of the sequential data and aims to provide recommendations that maximize the long-term reward. To this end, we train a farsighted recommender by using an offline RL algorithm with the policy network in our model architecture that has been initialized from a pre-trained transformer model. The pre-trained model leverages the superb ability of the transformer to process sequential information. Compared to prior works that rely on online interaction via simulation, we focus on implementing a fully offline RL framework that is able to converge in a fast and stable way. Through extensive experiments on public datasets, we show that our method is robust across various recommendation regimes, including e-commerce and movie suggestions. Compared to state-of-the-art supervised learning algorithms, our algorithm yields recommendations of higher quality, demonstrating the clear advantage of combining RL and transformers.

Matrix Estimation for Offline Reinforcement Learning with Low-Rank Structure

We consider offline Reinforcement Learning (RL), where the agent does not interact with the environment and must rely on offline data collected using a behavior policy. Previous works provide policy evaluation guarantees when the target policy to be evaluated is covered by the behavior policy, that is, state-action pairs visited by the target policy must also be visited by the behavior policy. We show that when the MDP has a latent low-rank structure, this coverage condition can be relaxed. Building on the connection to weighted matrix completion with non-uniform observations, we propose an offline policy evaluation algorithm that leverages the low-rank structure to estimate the values of uncovered state-action pairs. Our algorithm does not require a known feature representation, and our finite-sample error bound involves a novel discrepancy measure quantifying the discrepancy between the behavior and target policies in the spectral space. We provide concrete examples where our algorithm achieves accurate estimation while existing coverage conditions are not satisfied. Building on the above evaluation algorithm, we further design an offline policy optimization algorithm and provide non-asymptotic performance guarantees.

Likelihood Landscape and Local Minima Structures of Gaussian Mixture Models

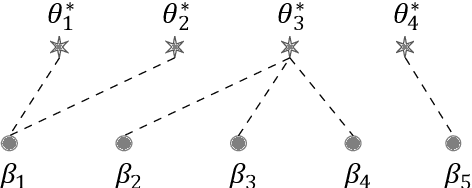
In this paper, we study the landscape of the population negative log-likelihood function of Gaussian Mixture Models with a general number of components. Due to nonconvexity, there exist multiple local minima that are not globally optimal, even when the mixture is well-separated. We show that all local minima share the same form of structure that partially identifies the component centers of the true mixture, in the sense that each local minimum involves a non-overlapping combination of fitting multiple Gaussians to a single true component and fitting a single Gaussian to multiple true components. Our results apply to the setting where the true mixture components satisfy a certain separation condition, and are valid even when the number of components is over-or under-specified. For Gaussian mixtures with three components, we obtain sharper results in terms of the scaling with the separation between the components.