Gradient Flows and Riemannian Structure in the Gromov-Wasserstein Geometry

The Wasserstein space of probability measures is known for its intricate Riemannian structure, which underpins the Wasserstein geometry and enables gradient flow algorithms. However, the Wasserstein geometry may not be suitable for certain tasks or data modalities. Motivated by scenarios where the global structure of the data needs to be preserved, this work initiates the study of gradient flows and Riemannian structure in the Gromov-Wasserstein (GW) geometry, which is particularly suited for such purposes. We focus on the inner product GW (IGW) distance between distributions on $\mathbb{R}^d$. Given a functional $\mathsf{F}:\mathcal{P}_2(\mathbb{R}^d)\to\mathbb{R}$ to optimize, we present an implicit IGW minimizing movement scheme that generates a sequence of distributions $\{\rho_i\}_{i=0}^n$, which are close in IGW and aligned in the 2-Wasserstein sense. Taking the time step to zero, we prove that the discrete solution converges to an IGW generalized minimizing movement (GMM) $(\rho_t)_t$ that follows the continuity equation with a velocity field $v_t\in L^2(\rho_t;\mathbb{R}^d)$, specified by a global transformation of the Wasserstein gradient of $\mathsf{F}$. The transformation is given by a mobility operator that modifies the Wasserstein gradient to encode not only local information, but also global structure. Our gradient flow analysis leads us to identify the Riemannian structure that gives rise to the intrinsic IGW geometry, using which we establish a Benamou-Brenier-like formula for IGW. We conclude with a formal derivation, akin to the Otto calculus, of the IGW gradient as the inverse mobility acting on the Wasserstein gradient. Numerical experiments validating our theory and demonstrating the global nature of IGW interpolations are provided.

Quantized Side Tuning: Fast and Memory-Efficient Tuning of Quantized Large Language Models

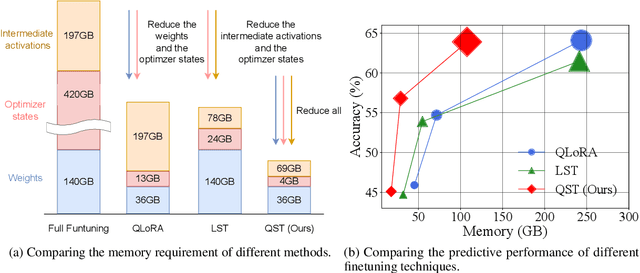
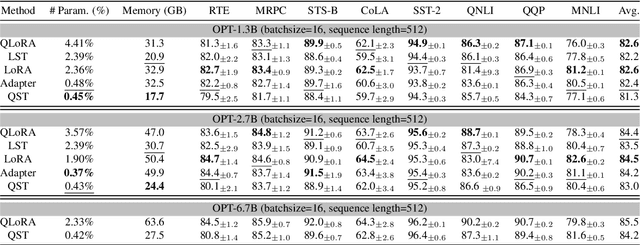
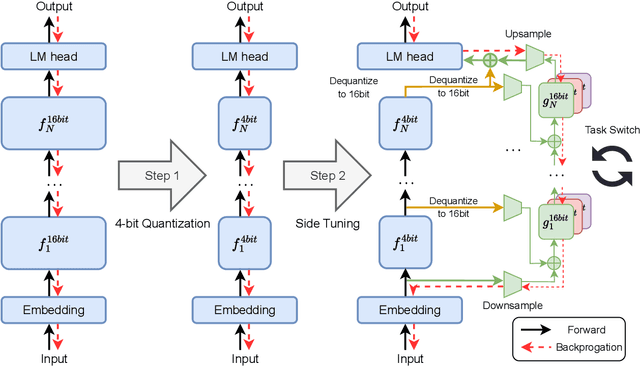
Finetuning large language models (LLMs) has been empirically effective on a variety of downstream tasks. Existing approaches to finetuning an LLM either focus on parameter-efficient finetuning, which only updates a small number of trainable parameters, or attempt to reduce the memory footprint during the training phase of the finetuning. Typically, the memory footprint during finetuning stems from three contributors: model weights, optimizer states, and intermediate activations. However, existing works still require considerable memory and none can simultaneously mitigate memory footprint for all three sources. In this paper, we present Quantized Side Tuing (QST), which enables memory-efficient and fast finetuning of LLMs by operating through a dual-stage process. First, QST quantizes an LLM's model weights into 4-bit to reduce the memory footprint of the LLM's original weights; QST also introduces a side network separated from the LLM, which utilizes the hidden states of the LLM to make task-specific predictions. Using a separate side network avoids performing backpropagation through the LLM, thus reducing the memory requirement of the intermediate activations. Furthermore, QST leverages several low-rank adaptors and gradient-free downsample modules to significantly reduce the trainable parameters, so as to save the memory footprint of the optimizer states. Experiments show that QST can reduce the total memory footprint by up to 2.3 $\times$ and speed up the finetuning process by up to 3 $\times$ while achieving competent performance compared with the state-of-the-art. When it comes to full finetuning, QST can reduce the total memory footprint up to 7 $\times$.

Cycle Consistent Probability Divergences Across Different Spaces

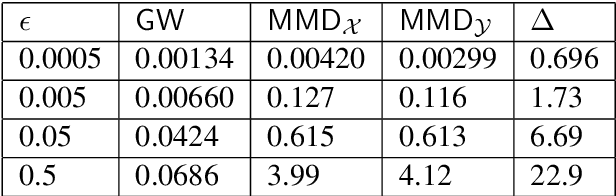
Discrepancy measures between probability distributions are at the core of statistical inference and machine learning. In many applications, distributions of interest are supported on different spaces, and yet a meaningful correspondence between data points is desired. Motivated to explicitly encode consistent bidirectional maps into the discrepancy measure, this work proposes a novel unbalanced Monge optimal transport formulation for matching, up to isometries, distributions on different spaces. Our formulation arises as a principled relaxation of the Gromov-Haussdroff distance between metric spaces, and employs two cycle-consistent maps that push forward each distribution onto the other. We study structural properties of the proposed discrepancy and, in particular, show that it captures the popular cycle-consistent generative adversarial network (GAN) framework as a special case, thereby providing the theory to explain it. Motivated by computational efficiency, we then kernelize the discrepancy and restrict the mappings to parametric function classes. The resulting kernelized version is coined the generalized maximum mean discrepancy (GMMD). Convergence rates for empirical estimation of GMMD are studied and experiments to support our theory are provided.

Non-Asymptotic Performance Guarantees for Neural Estimation of $\mathsf{f}$-Divergences

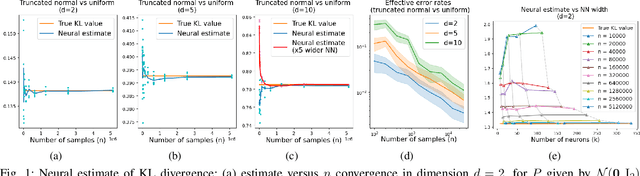
Statistical distances (SDs), which quantify the dissimilarity between probability distributions, are central to machine learning and statistics. A modern method for estimating such distances from data relies on parametrizing a variational form by a neural network (NN) and optimizing it. These estimators are abundantly used in practice, but corresponding performance guarantees are partial and call for further exploration. In particular, there seems to be a fundamental tradeoff between the two sources of error involved: approximation and estimation. While the former needs the NN class to be rich and expressive, the latter relies on controlling complexity. This paper explores this tradeoff by means of non-asymptotic error bounds, focusing on three popular choices of SDs -- Kullback-Leibler divergence, chi-squared divergence, and squared Hellinger distance. Our analysis relies on non-asymptotic function approximation theorems and tools from empirical process theory. Numerical results validating the theory are also provided.

Road Extraction by Deep Residual U-Net

Road extraction from aerial images has been a hot research topic in the field of remote sensing image analysis. In this letter, a semantic segmentation neural network which combines the strengths of residual learning and U-Net is proposed for road area extraction. The network is built with residual units and has similar architecture to that of U-Net. The benefits of this model is two-fold: first, residual units ease training of deep networks. Second, the rich skip connections within the network could facilitate information propagation, allowing us to design networks with fewer parameters however better performance. We test our network on a public road dataset and compare it with U-Net and other two state of the art deep learning based road extraction methods. The proposed approach outperforms all the comparing methods, which demonstrates its superiority over recently developed state of the arts.