Certifying Out-of-Domain Generalization for Blackbox Functions

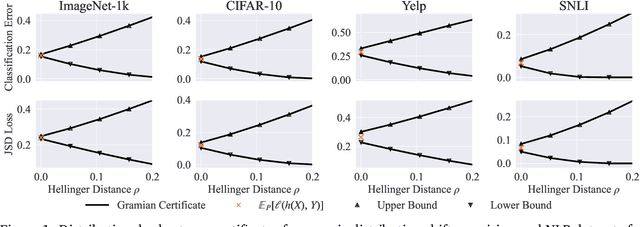
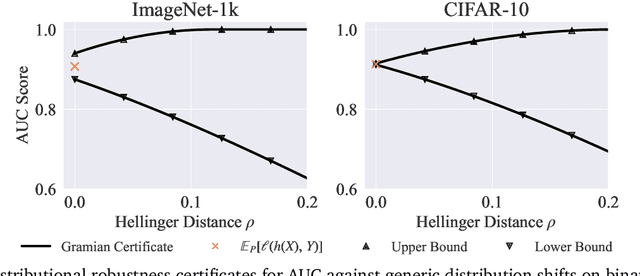
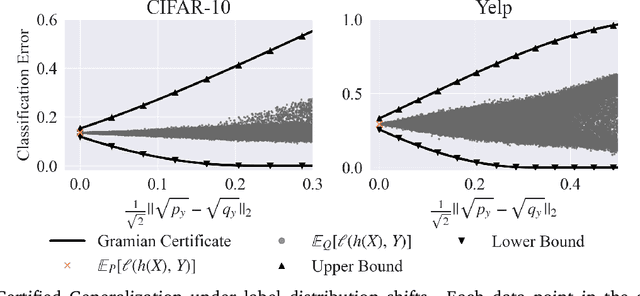
Certifying the robustness of model performance under bounded data distribution shifts has recently attracted intensive interests under the umbrella of distributional robustness. However, existing techniques either make strong assumptions on the model class and loss functions that can be certified, such as smoothness expressed via Lipschitz continuity of gradients, or require to solve complex optimization problems. As a result, the wider application of these techniques is currently limited by its scalability and flexibility -- these techniques often do not scale to large-scale datasets with modern deep neural networks or cannot handle loss functions which may be non-smooth, such as the 0-1 loss. In this paper, we focus on the problem of certifying distributional robustness for black box models and bounded losses, without other assumptions. We propose a novel certification framework given bounded distance of mean and variance of two distributions. Our certification technique scales to ImageNet-scale datasets, complex models, and a diverse range of loss functions. We then focus on one specific application enabled by such scalability and flexibility, i.e., certifying out-of-domain generalization for large neural networks and loss functions such as accuracy and AUC. We experimentally validate our certification method on a number of datasets, ranging from ImageNet, where we provide the first non-vacuous certified out-of-domain generalization, to smaller classification tasks where we are able to compare with the state-of-the-art and show that our method performs considerably better.

Optimal Provable Robustness of Quantum Classification via Quantum Hypothesis Testing

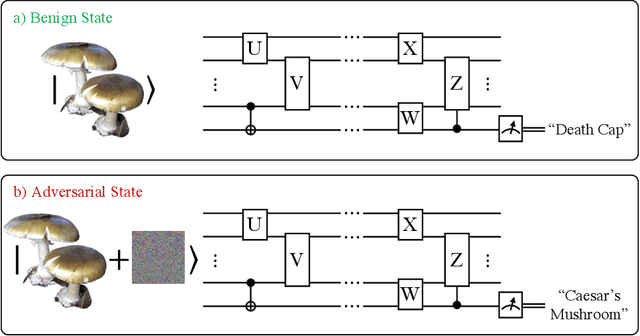
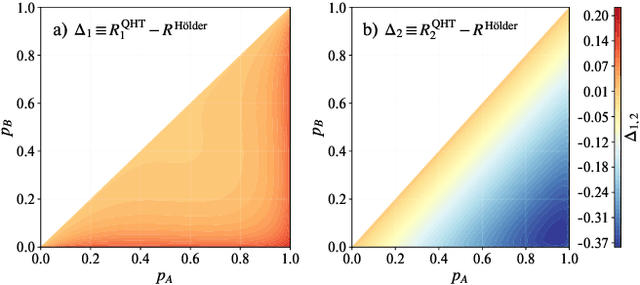
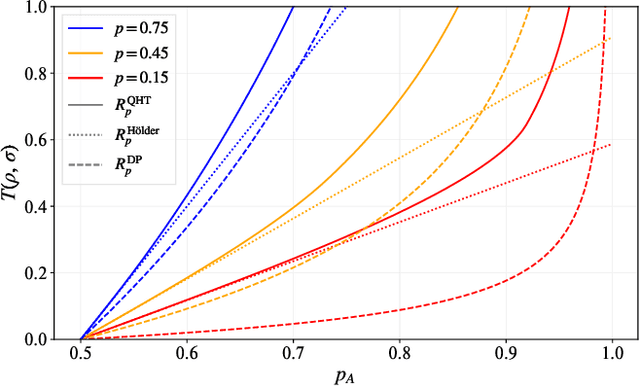
Quantum machine learning models have the potential to offer speedups and better predictive accuracy compared to their classical counterparts. However, these quantum algorithms, like their classical counterparts, have been shown to also be vulnerable to input perturbations, in particular for classification problems. These can arise either from noisy implementations or, as a worst-case type of noise, adversarial attacks. These attacks can undermine both the reliability and security of quantum classification algorithms. In order to develop defence mechanisms and to better understand the reliability of these algorithms, it is crucial to understand their robustness properties in presence of both natural noise sources and adversarial manipulation. From the observation that, unlike in the classical setting, measurements involved in quantum classification algorithms are naturally probabilistic, we uncover and formalize a fundamental link between binary quantum hypothesis testing (QHT) and provably robust quantum classification. Then from the optimality of QHT, we prove a robustness condition, which is tight under modest assumptions, and enables us to develop a protocol to certify robustness. Since this robustness condition is a guarantee against the worst-case noise scenarios, our result naturally extends to scenarios in which the noise source is known. Thus we also provide a framework to study the reliability of quantum classification protocols under more general settings.

End-to-end Robustness for Sensing-Reasoning Machine Learning Pipelines

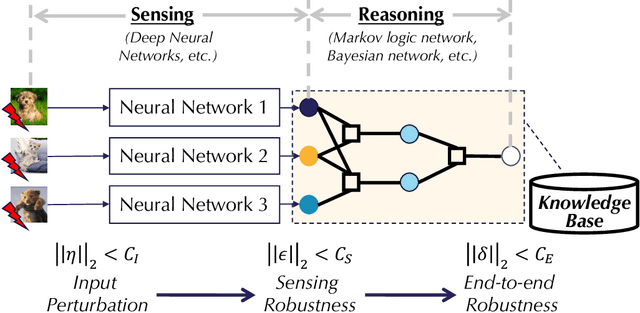
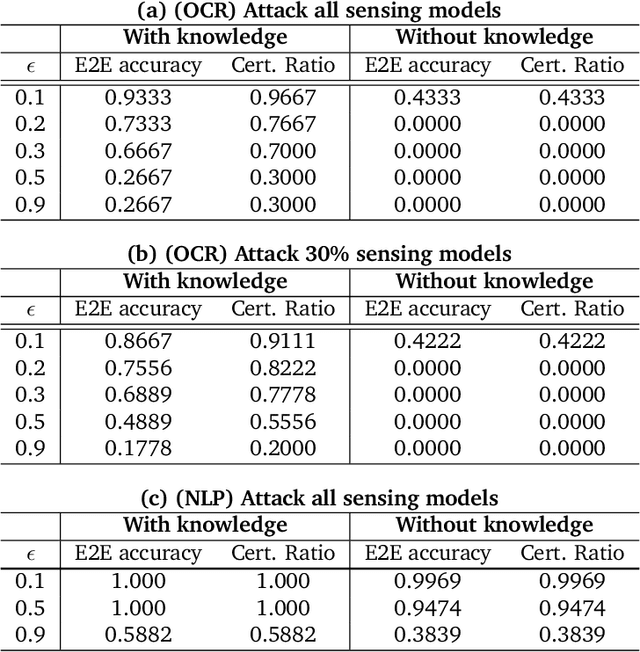
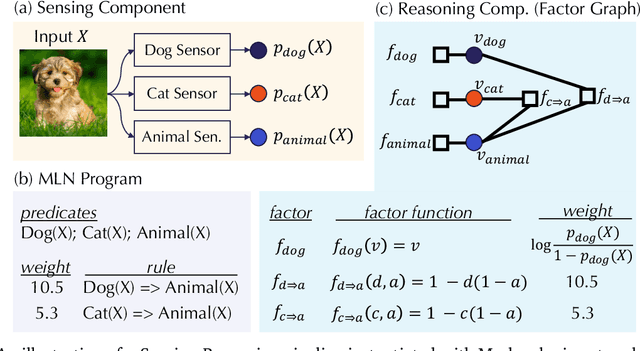
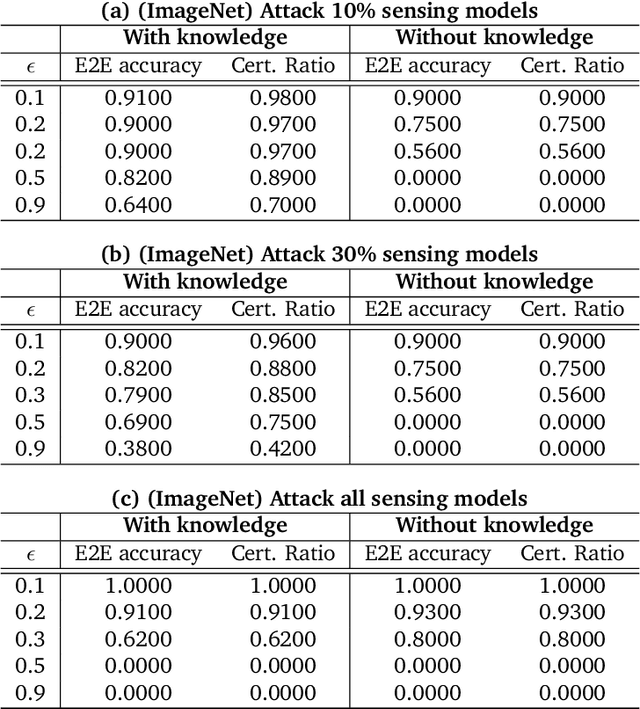
As machine learning (ML) being applied to many mission-critical scenarios, certifying ML model robustness becomes increasingly important. Many previous works focuses on the robustness of independent ML and ensemble models, and can only certify a very small magnitude of the adversarial perturbation. In this paper, we take a different viewpoint and improve learning robustness by going beyond independent ML and ensemble models. We aim at promoting the generic Sensing-Reasoning machine learning pipeline which contains both the sensing (e.g. deep neural networks) and reasoning (e.g. Markov logic networks (MLN)) components enriched with domain knowledge. Can domain knowledge help improve learning robustness? Can we formally certify the end-to-end robustness of such an ML pipeline? We first theoretically analyze the computational complexity of checking the provable robustness in the reasoning component. We then derive the provable robustness bound for several concrete reasoning components. We show that for reasoning components such as MLN and a specific family of Bayesian networks it is possible to certify the robustness of the whole pipeline even with a large magnitude of perturbation which cannot be certified by existing work. Finally, we conduct extensive real-world experiments on large scale datasets to evaluate the certified robustness for Sensing-Reasoning ML pipelines.

Bayesian Deep Learning on a Quantum Computer

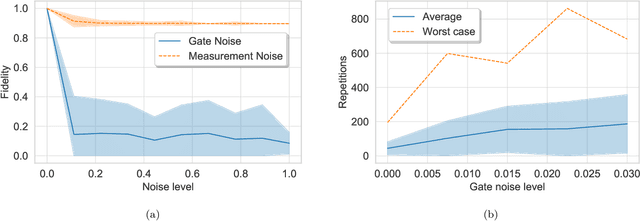
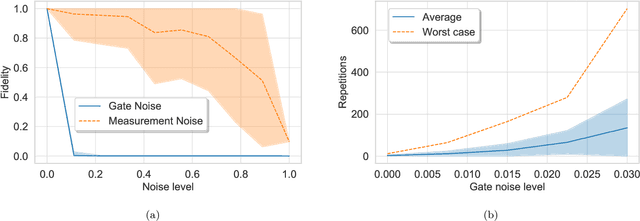
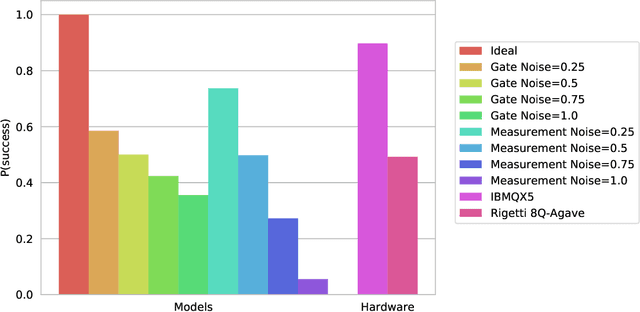
Bayesian methods in machine learning, such as Gaussian processes, have great advantages compared to other techniques. In particular, they provide estimates of the uncertainty associated with a prediction. Extending the Bayesian approach to deep architectures has remained a major challenge. Recent results connected deep feedforward neural networks with Gaussian processes, allowing training without backpropagation. This connection enables us to leverage a quantum algorithm designed for Gaussian processes and develop a new algorithm for Bayesian deep learning on quantum computers. The properties of the kernel matrix in the Gaussian process ensure the efficient execution of the core component of the protocol, quantum matrix inversion, providing an at least polynomial speedup over the classical algorithm. Furthermore, we demonstrate the execution of the algorithm on contemporary quantum computers and analyze its robustness with respect to realistic noise models.

A note on state preparation for quantum machine learning

The intersection between the fields of machine learning and quantum information processing is proving to be a fruitful field for the discovery of new quantum algorithms, which potentially offer an exponential speed-up over their classical counterparts. However, many such algorithms require the ability to produce states proportional to vectors stored in quantum memory. Even given access to quantum databases which store exponentially long vectors, the construction of which is considered a one-off overhead, it has been argued that the cost of preparing such amplitude-encoded states may offset any exponential quantum advantage. Here we argue that specifically in the context of machine learning applications it suffices to prepare a state close to the ideal state only in the $\infty$-norm, and that this can be achieved with only a constant number of memory queries.

Quantum algorithms for training Gaussian Processes

Gaussian processes (GPs) are important models in supervised machine learning. Training in Gaussian processes refers to selecting the covariance functions and the associated parameters in order to improve the outcome of predictions, the core of which amounts to evaluating the logarithm of the marginal likelihood (LML) of a given model. LML gives a concrete measure of the quality of prediction that a GP model is expected to achieve. The classical computation of LML typically carries a polynomial time overhead with respect to the input size. We propose a quantum algorithm that computes the logarithm of the determinant of a Hermitian matrix, which runs in logarithmic time for sparse matrices. This is applied in conjunction with a variant of the quantum linear system algorithm that allows for logarithmic time computation of the form $\mathbf{y}^TA^{-1}\mathbf{y}$, where $\mathbf{y}$ is a dense vector and $A$ is the covariance matrix. We hence show that quantum computing can be used to estimate the LML of a GP with exponentially improved efficiency under certain conditions.

Quantum assisted Gaussian process regression

Gaussian processes (GP) are a widely used model for regression problems in supervised machine learning. Implementation of GP regression typically requires $O(n^3)$ logic gates. We show that the quantum linear systems algorithm [Harrow et al., Phys. Rev. Lett. 103, 150502 (2009)] can be applied to Gaussian process regression (GPR), leading to an exponential reduction in computation time in some instances. We show that even in some cases not ideally suited to the quantum linear systems algorithm, a polynomial increase in efficiency still occurs.