Certifying Out-of-Domain Generalization for Blackbox Functions

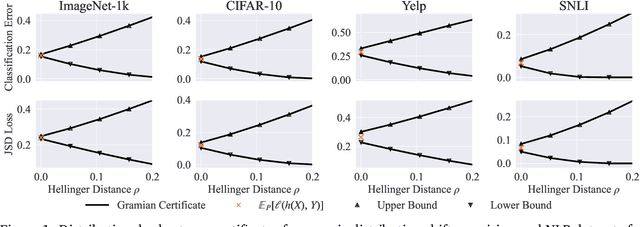
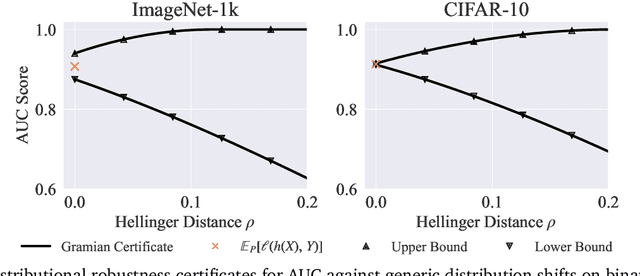
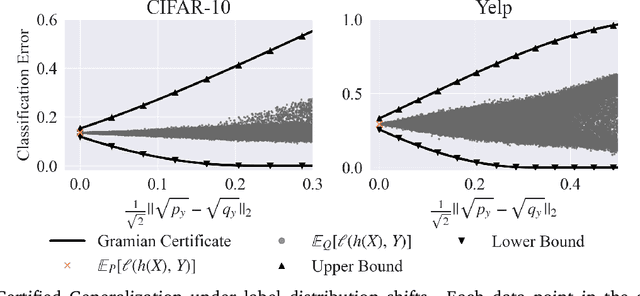
Certifying the robustness of model performance under bounded data distribution shifts has recently attracted intensive interests under the umbrella of distributional robustness. However, existing techniques either make strong assumptions on the model class and loss functions that can be certified, such as smoothness expressed via Lipschitz continuity of gradients, or require to solve complex optimization problems. As a result, the wider application of these techniques is currently limited by its scalability and flexibility -- these techniques often do not scale to large-scale datasets with modern deep neural networks or cannot handle loss functions which may be non-smooth, such as the 0-1 loss. In this paper, we focus on the problem of certifying distributional robustness for black box models and bounded losses, without other assumptions. We propose a novel certification framework given bounded distance of mean and variance of two distributions. Our certification technique scales to ImageNet-scale datasets, complex models, and a diverse range of loss functions. We then focus on one specific application enabled by such scalability and flexibility, i.e., certifying out-of-domain generalization for large neural networks and loss functions such as accuracy and AUC. We experimentally validate our certification method on a number of datasets, ranging from ImageNet, where we provide the first non-vacuous certified out-of-domain generalization, to smaller classification tasks where we are able to compare with the state-of-the-art and show that our method performs considerably better.