Bayesian Deep Learning on a Quantum Computer
Paper and Code
Jul 09, 2018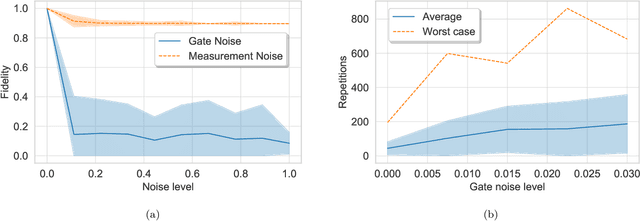
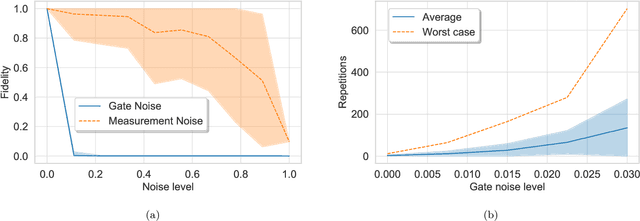
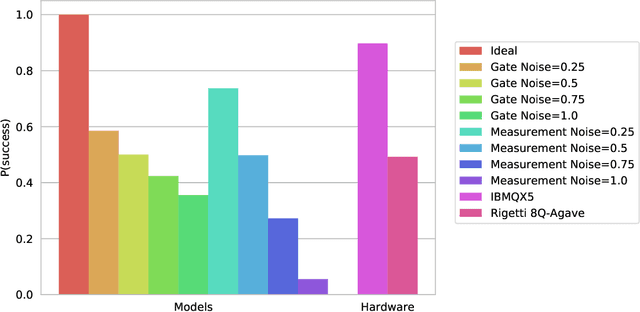
Bayesian methods in machine learning, such as Gaussian processes, have great advantages compared to other techniques. In particular, they provide estimates of the uncertainty associated with a prediction. Extending the Bayesian approach to deep architectures has remained a major challenge. Recent results connected deep feedforward neural networks with Gaussian processes, allowing training without backpropagation. This connection enables us to leverage a quantum algorithm designed for Gaussian processes and develop a new algorithm for Bayesian deep learning on quantum computers. The properties of the kernel matrix in the Gaussian process ensure the efficient execution of the core component of the protocol, quantum matrix inversion, providing an at least polynomial speedup over the classical algorithm. Furthermore, we demonstrate the execution of the algorithm on contemporary quantum computers and analyze its robustness with respect to realistic noise models.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge