Faster Stochastic First-Order Method for Maximum-Likelihood Quantum State Tomography
Paper and Code
Nov 23, 2022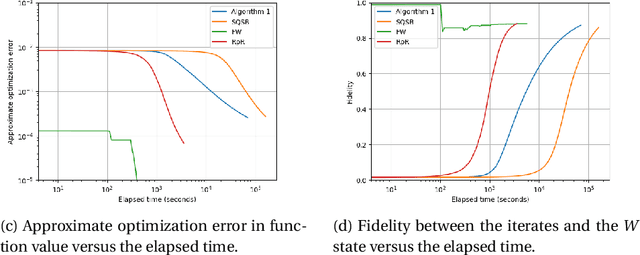
In maximum-likelihood quantum state tomography, both the sample size and dimension grow exponentially with the number of qubits. It is therefore desirable to develop a stochastic first-order method, just like stochastic gradient descent for modern machine learning, to compute the maximum-likelihood estimate. To this end, we propose an algorithm called stochastic mirror descent with the Burg entropy. Its expected optimization error vanishes at a $O ( \sqrt{ ( 1 / t ) d \log t } )$ rate, where $d$ and $t$ denote the dimension and number of iterations, respectively. Its per-iteration time complexity is $O ( d^3 )$, independent of the sample size. To the best of our knowledge, this is currently the computationally fastest stochastic first-order method for maximum-likelihood quantum state tomography.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge