Implicit Neural Representation for Physics-driven Actuated Soft Bodies

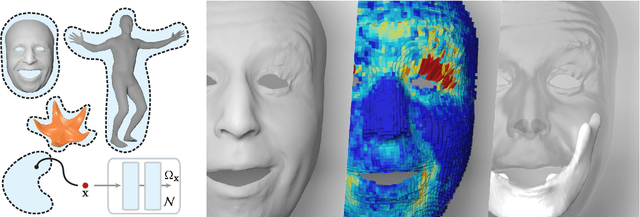
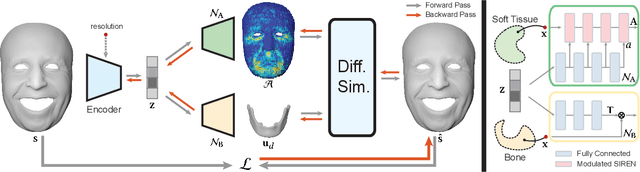
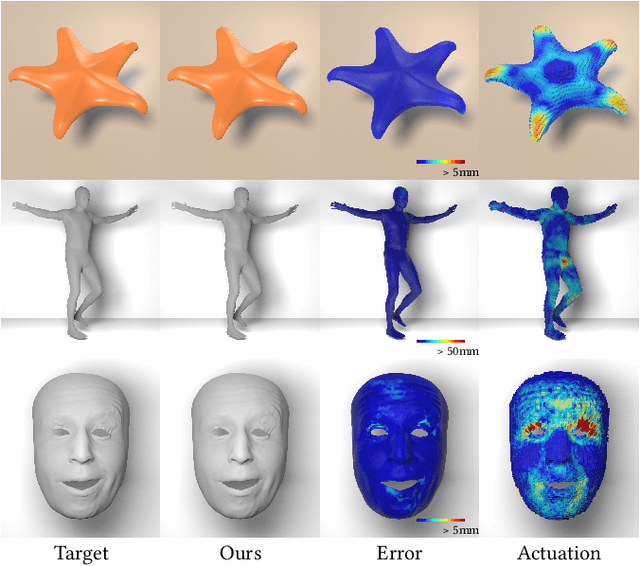
Active soft bodies can affect their shape through an internal actuation mechanism that induces a deformation. Similar to recent work, this paper utilizes a differentiable, quasi-static, and physics-based simulation layer to optimize for actuation signals parameterized by neural networks. Our key contribution is a general and implicit formulation to control active soft bodies by defining a function that enables a continuous mapping from a spatial point in the material space to the actuation value. This property allows us to capture the signal's dominant frequencies, making the method discretization agnostic and widely applicable. We extend our implicit model to mandible kinematics for the particular case of facial animation and show that we can reliably reproduce facial expressions captured with high-quality capture systems. We apply the method to volumetric soft bodies, human poses, and facial expressions, demonstrating artist-friendly properties, such as simple control over the latent space and resolution invariance at test time.

Scalable Learning-Based Sampling Optimization for Compressive Dynamic MRI

Slow acquisition has been one of the historical problems in dynamic magnetic resonance imaging (dMRI), but the rise of compressed sensing (CS) has brought numerous algorithms that successfully achieve high acceleration rates. While CS proposes random sampling for data acquisition, practical CS applications to dMRI have typically relied on random variable-density (VD) sampling patterns, where masks are drawn from probabilistic models, which preferably sample from the center of the Fourier domain. In contrast to this model-driven approach, we propose the first data-driven, scalable framework for optimizing sampling patterns in dMRI. Through a greedy algorithm, this approach allows the data to directly govern the search for a mask that exhibits good empirical performance. Previous greedy approach, designed for static MRI, required very intensive computations, prohibiting their direct application to dMRI, and we address this issue by resorting to a stochastic greedy algorithm that exploits only a fraction of resources compared to the previous approach without sacrificing the reconstruction accuracy. A thorough comparison on in vivo datasets shows the inefficiency of model-based approaches in terms of sampling performance and suggests that our data-driven sampling approach could fully enable the potential of CS applied to dMRI.

Learning-Based Compressive MRI

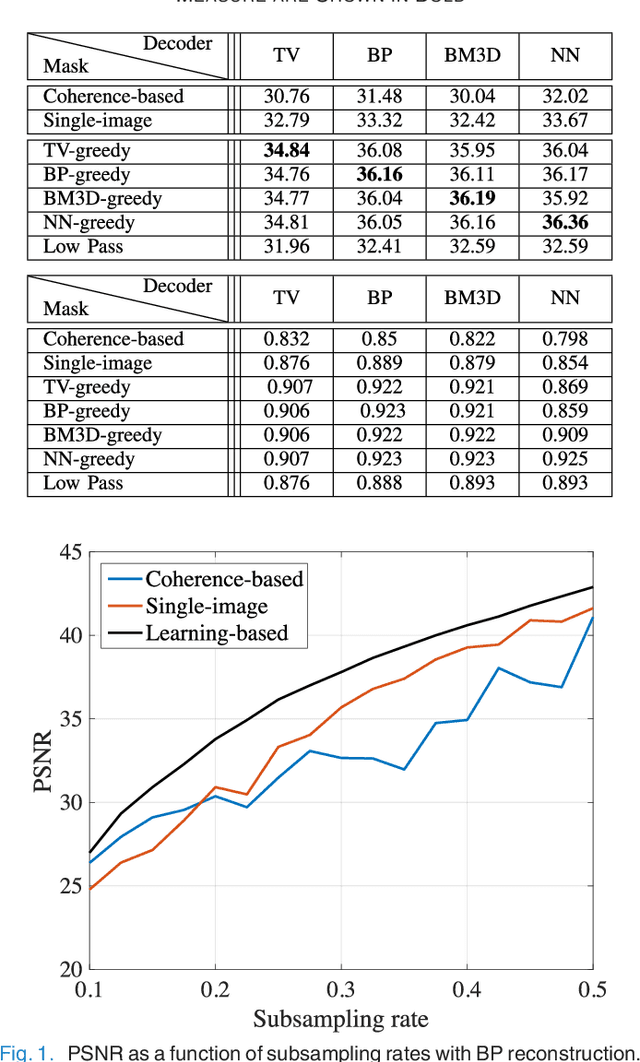
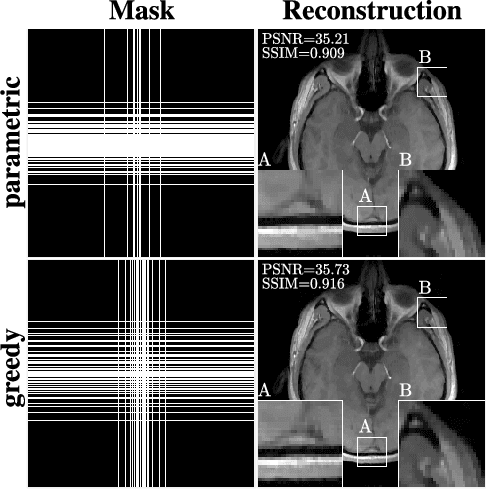
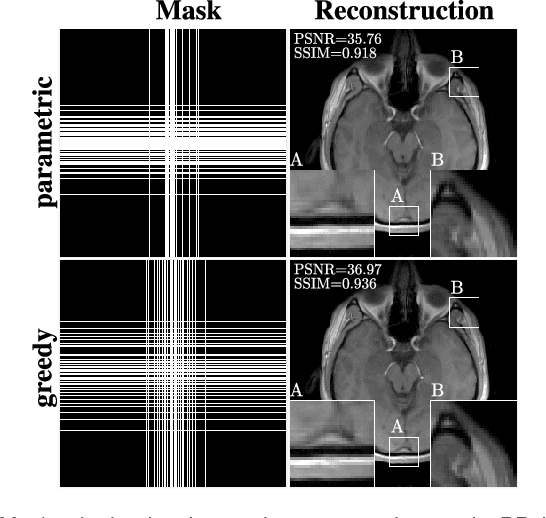
In the area of magnetic resonance imaging (MRI), an extensive range of non-linear reconstruction algorithms have been proposed that can be used with general Fourier subsampling patterns. However, the design of these subsampling patterns has typically been considered in isolation from the reconstruction rule and the anatomy under consideration. In this paper, we propose a learning-based framework for optimizing MRI subsampling patterns for a specific reconstruction rule and anatomy, considering both the noiseless and noisy settings. Our learning algorithm has access to a representative set of training signals, and searches for a sampling pattern that performs well on average for the signals in this set. We present a novel parameter-free greedy mask selection method, and show it to be effective for a variety of reconstruction rules and performance metrics. Moreover we also support our numerical findings by providing a rigorous justification of our framework via statistical learning theory.

Learning-based Compressive Subsampling

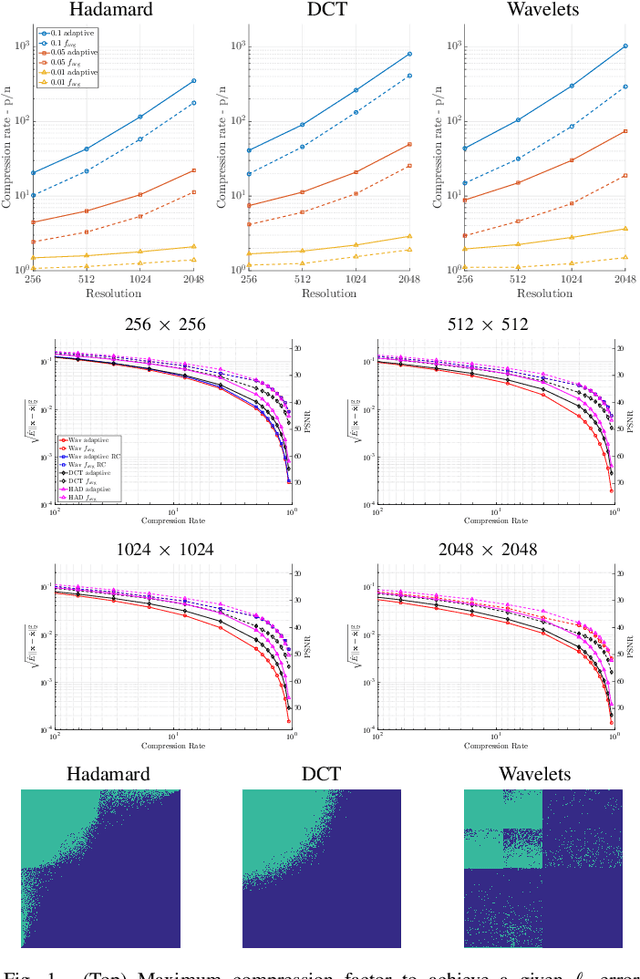
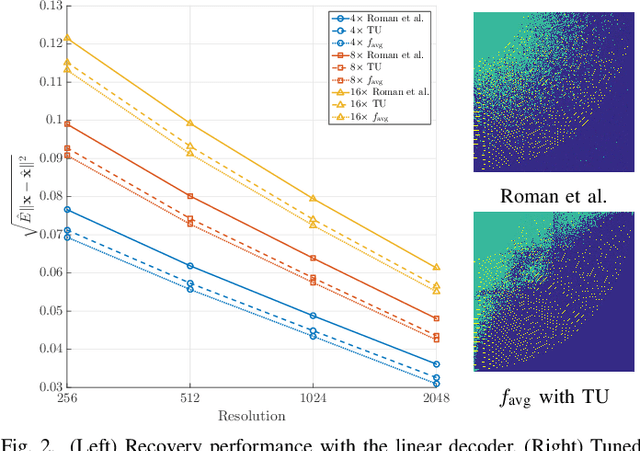
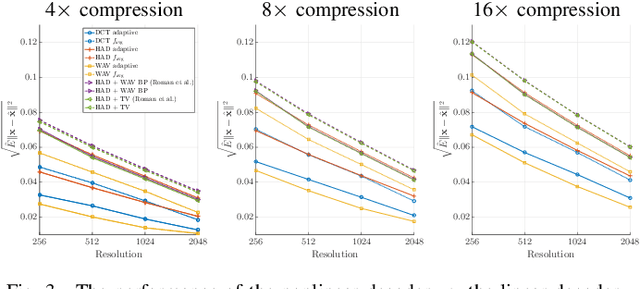
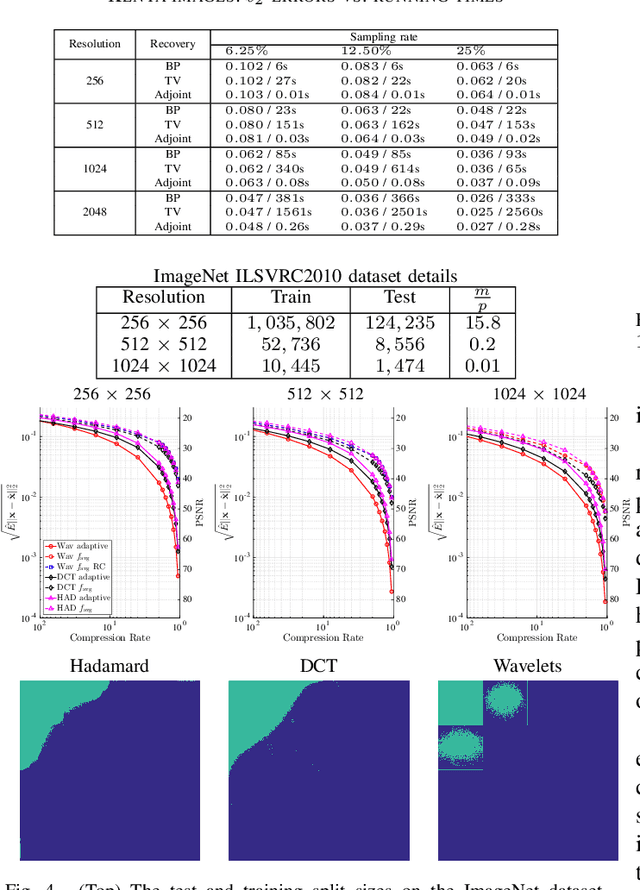
The problem of recovering a structured signal $\mathbf{x} \in \mathbb{C}^p$ from a set of dimensionality-reduced linear measurements $\mathbf{b} = \mathbf {A}\mathbf {x}$ arises in a variety of applications, such as medical imaging, spectroscopy, Fourier optics, and computerized tomography. Due to computational and storage complexity or physical constraints imposed by the problem, the measurement matrix $\mathbf{A} \in \mathbb{C}^{n \times p}$ is often of the form $\mathbf{A} = \mathbf{P}_{\Omega}\boldsymbol{\Psi}$ for some orthonormal basis matrix $\boldsymbol{\Psi}\in \mathbb{C}^{p \times p}$ and subsampling operator $\mathbf{P}_{\Omega}: \mathbb{C}^{p} \rightarrow \mathbb{C}^{n}$ that selects the rows indexed by $\Omega$. This raises the fundamental question of how best to choose the index set $\Omega$ in order to optimize the recovery performance. Previous approaches to addressing this question rely on non-uniform \emph{random} subsampling using application-specific knowledge of the structure of $\mathbf{x}$. In this paper, we instead take a principled learning-based approach in which a \emph{fixed} index set is chosen based on a set of training signals $\mathbf{x}_1,\dotsc,\mathbf{x}_m$. We formulate combinatorial optimization problems seeking to maximize the energy captured in these signals in an average-case or worst-case sense, and we show that these can be efficiently solved either exactly or approximately via the identification of modularity and submodularity structures. We provide both deterministic and statistical theoretical guarantees showing how the resulting measurement matrices perform on signals differing from the training signals, and we provide numerical examples showing our approach to be effective on a variety of data sets.