Benchmarking Floworks against OpenAI & Anthropic: A Novel Framework for Enhanced LLM Function Calling

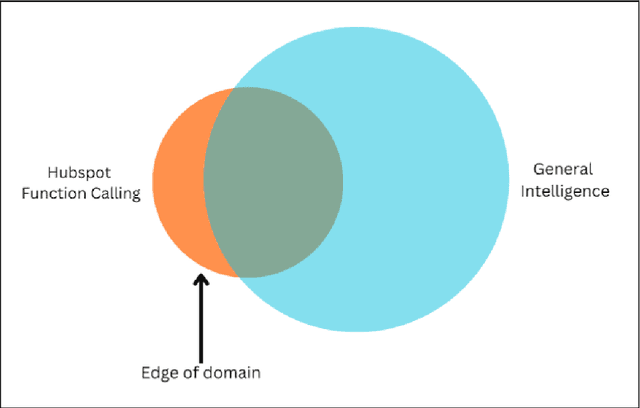
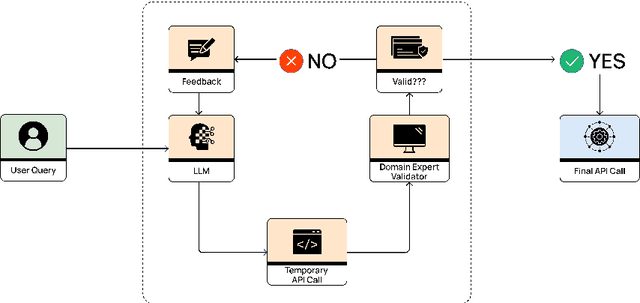
Large Language Models (LLMs) have shown remarkable capabilities in various domains, yet their economic impact has been limited by challenges in tool use and function calling. This paper introduces ThorV2, a novel architecture that significantly enhances LLMs' function calling abilities. We develop a comprehensive benchmark focused on HubSpot CRM operations to evaluate ThorV2 against leading models from OpenAI and Anthropic. Our results demonstrate that ThorV2 outperforms existing models in accuracy, reliability, latency, and cost efficiency for both single and multi-API calling tasks. We also show that ThorV2 is far more reliable and scales better to multistep tasks compared to traditional models. Our work offers the tantalizing possibility of more accurate function-calling compared to today's best-performing models using significantly smaller LLMs. These advancements have significant implications for the development of more capable AI assistants and the broader application of LLMs in real-world scenarios.

Group-Sparse Model Selection: Hardness and Relaxations

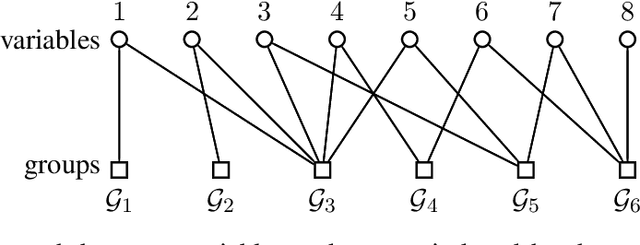
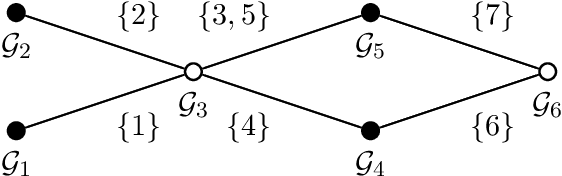
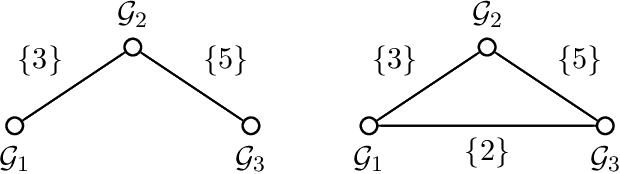
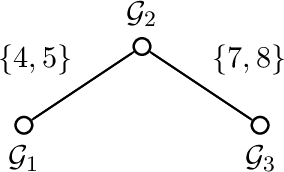
Group-based sparsity models are proven instrumental in linear regression problems for recovering signals from much fewer measurements than standard compressive sensing. The main promise of these models is the recovery of "interpretable" signals through the identification of their constituent groups. In this paper, we establish a combinatorial framework for group-model selection problems and highlight the underlying tractability issues. In particular, we show that the group-model selection problem is equivalent to the well-known NP-hard weighted maximum coverage problem (WMC). Leveraging a graph-based understanding of group models, we describe group structures which enable correct model selection in polynomial time via dynamic programming. Furthermore, group structures that lead to totally unimodular constraints have tractable discrete as well as convex relaxations. We also present a generalization of the group-model that allows for within group sparsity, which can be used to model hierarchical sparsity. Finally, we study the Pareto frontier of group-sparse approximations for two tractable models, among which the tree sparsity model, and illustrate selection and computation trade-offs between our framework and the existing convex relaxations.