Optimal Computational Trade-Off of Inexact Proximal Methods
Paper and Code
Oct 21, 2012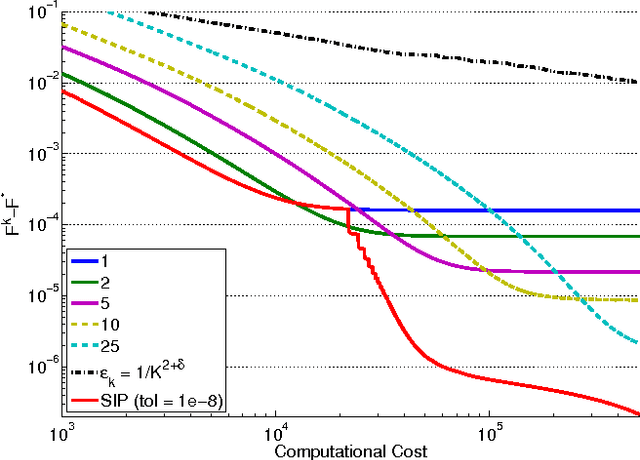
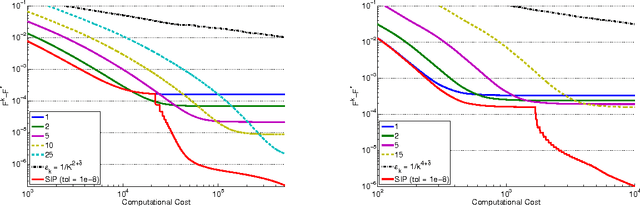
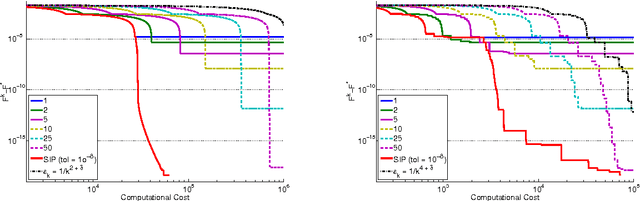
In this paper, we investigate the trade-off between convergence rate and computational cost when minimizing a composite functional with proximal-gradient methods, which are popular optimisation tools in machine learning. We consider the case when the proximity operator is computed via an iterative procedure, which provides an approximation of the exact proximity operator. In that case, we obtain algorithms with two nested loops. We show that the strategy that minimizes the computational cost to reach a solution with a desired accuracy in finite time is to set the number of inner iterations to a constant, which differs from the strategy indicated by a convergence rate analysis. In the process, we also present a new procedure called SIP (that is Speedy Inexact Proximal-gradient algorithm) that is both computationally efficient and easy to implement. Our numerical experiments confirm the theoretical findings and suggest that SIP can be a very competitive alternative to the standard procedure.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge