Compressive Closeness in Networks
Paper and Code
Jun 19, 2019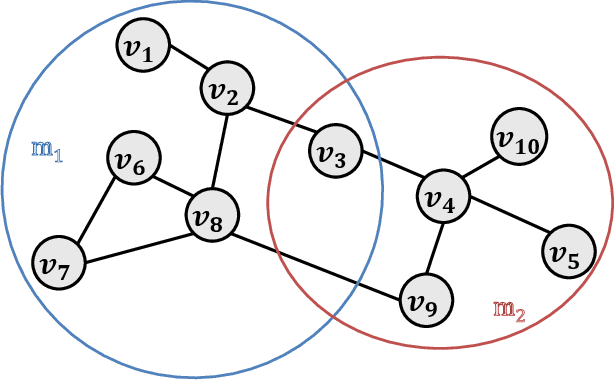
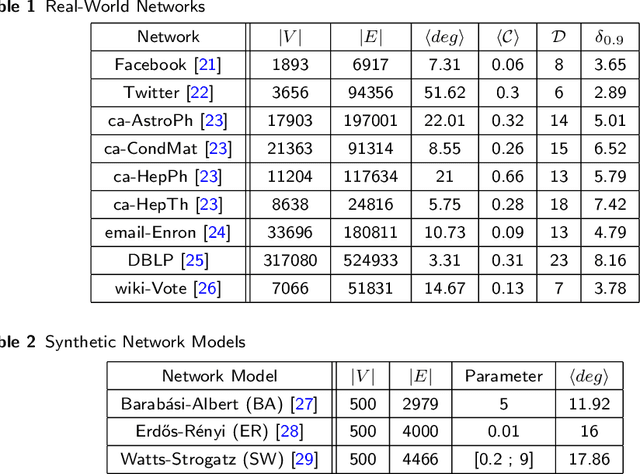
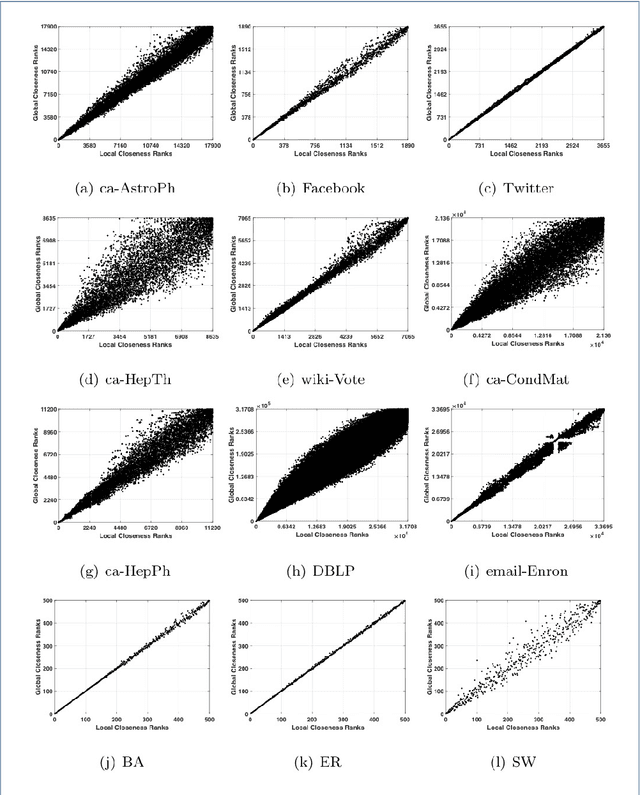
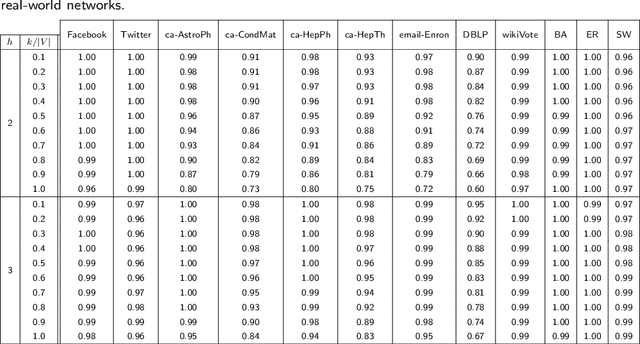
Distributed algorithms for network science applications are of great importance due to today's large real-world networks. In such algorithms, a node is allowed only to have local interactions with its immediate neighbors. This is because the whole network topological structure is often unknown to each node. Recently, distributed detection of central nodes, concerning different notions of importance, within a network has received much attention. Closeness centrality is a prominent measure to evaluate the importance (influence) of nodes, based on their accessibility, in a given network. In this paper, first, we introduce a local (ego-centric) metric that correlates well with the global closeness centrality; however, it has very low computational complexity. Second, we propose a compressive sensing (CS)-based framework to accurately recover high closeness centrality nodes in the network utilizing the proposed local metric. Both ego-centric metric computation and its aggregation via CS are efficient and distributed, using only local interactions between neighboring nodes. Finally, we evaluate the performance of the proposed method through extensive experiments on various synthetic and real-world networks. The results show that the proposed local metric correlates with the global closeness centrality, better than the current local metrics. Moreover, the results demonstrate that the proposed CS-based method outperforms the state-of-the-art methods with notable improvement.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge