Distributed Beam Alignment in sub-THz D2D Networks

Devices in a device-to-device (D2D) network operating in sub-THz frequencies require knowledge of the spatial channel that connects them to their peers. Acquiring such high dimensional channel state information entails large overhead, which drastically increases with the number of network devices. In this paper, we propose an accelerated method to achieve network-wide beam alignment in an efficient way. To this aim, we consider compressed sensing estimation enabled by a novel design of pilot sequences. Our designed pilots have constant envelope to alleviate hardware requirements at the transmitters, while they exhibit a "comb-like"' spectrum that flexibly allocates energy only on certain frequencies. This design enables multiple devices to transmit thier pilots concurrently while remaining orthogonal in frequency, achieving simultaneous alignment of multiple devices. Furthermore, we present a sequential partitioning strategy into transmitters and receivers that results in logarithmic scaling of the overhead with the number of devices, as opposed to the conventional linear scaling. Finally, we show via accurate modeling of the indoor propagation environment and ray tracing simulations that the resulting sub-THz channels after successful beamforming are approximately frequency flat, therefore suitable for efficient single carrier transmission without equalization. We compare our results against an "802.11ad inspired" baseline and show that our method is capable to greatly reduce the number of pilots required to achieve network-wide alignment.

A Deep Unfolding-Based Scalarization Approach for Power Control in D2D Networks

Optimizing network utility in device-to-device networks is typically formulated as a non-convex optimization problem. This paper addresses the scenario where the optimization variables are from a bounded but continuous set, allowing each device to perform power control. The power at each link is optimized to maximize a desired network utility. Specifically, we consider the weighted-sum-rate. The state of the art benchmark for this problem is fractional programming with quadratic transform, known as FPLinQ. We propose a scalarization approach to transform the weighted-sum-rate, developing an iterative algorithm that depends on step sizes, a reference, and a direction vector. By employing the deep unfolding approach, we optimize these parameters by presenting the iterative algorithm as a finite sequence of steps, enabling it to be trained as a deep neural network. Numerical experiments demonstrate that the unfolded algorithm performs comparably to the benchmark in most cases while exhibiting lower complexity. Furthermore, the unfolded algorithm shows strong generalizability in terms of varying the number of users, the signal-to-noise ratio and arbitrary weights. The weighted-sum-rate maximizer can be integrated into a low-complexity fairness scheduler, updating priority weights via virtual queues and Lyapunov Drift Plus Penalty. This is demonstrated through experiments using proportional and max-min fairness.

A physics-informed neural network framework for modeling obstacle-related equations

Deep learning has been highly successful in some applications. Nevertheless, its use for solving partial differential equations (PDEs) has only been of recent interest with current state-of-the-art machine learning libraries, e.g., TensorFlow or PyTorch. Physics-informed neural networks (PINNs) are an attractive tool for solving partial differential equations based on sparse and noisy data. Here extend PINNs to solve obstacle-related PDEs which present a great computational challenge because they necessitate numerical methods that can yield an accurate approximation of the solution that lies above a given obstacle. The performance of the proposed PINNs is demonstrated in multiple scenarios for linear and nonlinear PDEs subject to regular and irregular obstacles.

Photothermal-SR-Net: A Customized Deep Unfolding Neural Network for Photothermal Super Resolution Imaging

This paper presents deep unfolding neural networks to handle inverse problems in photothermal radiometry enabling super resolution (SR) imaging. Photothermal imaging is a well-known technique in active thermography for nondestructive inspection of defects in materials such as metals or composites. A grand challenge of active thermography is to overcome the spatial resolution limitation imposed by heat diffusion in order to accurately resolve each defect. The photothermal SR approach enables to extract high-frequency spatial components based on the deconvolution with the thermal point spread function. However, stable deconvolution can only be achieved by using the sparse structure of defect patterns, which often requires tedious, hand-crafted tuning of hyperparameters and results in computationally intensive algorithms. On this account, Photothermal-SR-Net is proposed in this paper, which performs deconvolution by deep unfolding considering the underlying physics. This enables to super resolve 2D thermal images for nondestructive testing with a substantially improved convergence rate. Since defects appear sparsely in materials, Photothermal-SR-Net applies trained block-sparsity thresholding to the acquired thermal images in each convolutional layer. The performance of the proposed approach is evaluated and discussed using various deep unfolding and thresholding approaches applied to 2D thermal images. Subsequently, studies are conducted on how to increase the reconstruction quality and the computational performance of Photothermal-SR-Net is evaluated. Thereby, it was found that the computing time for creating high-resolution images could be significantly reduced without decreasing the reconstruction quality by using pixel binning as a preprocessing step.

Learned Block Iterative Shrinkage Thresholding Algorithm for Photothermal Super Resolution Imaging

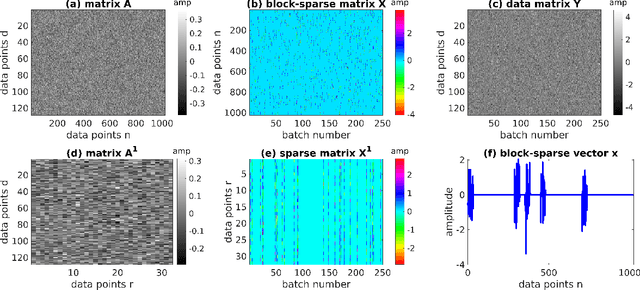
Block-sparse regularization is already well-known in active thermal imaging and is used for multiple measurement based inverse problems. The main bottleneck of this method is the choice of regularization parameters which differs for each experiment. To avoid time-consuming manually selected regularization parameter, we propose a learned block-sparse optimization approach using an iterative algorithm unfolded into a deep neural network. More precisely, we show the benefits of using a learned block iterative shrinkage thresholding algorithm that is able to learn the choice of regularization parameters. In addition, this algorithm enables the determination of a suitable weight matrix to solve the underlying inverse problem. Therefore, in this paper we present the algorithm and compare it with state of the art block iterative shrinkage thresholding using synthetically generated test data and experimental test data from active thermography for defect reconstruction. Our results show that the use of the learned block-sparse optimization approach provides smaller normalized mean square errors for a small fixed number of iterations than without learning. Thus, this new approach allows to improve the convergence speed and only needs a few iterations to generate accurate defect reconstruction in photothermal super resolution imaging.