Learning deep linear neural networks: Riemannian gradient flows and convergence to global minimizers

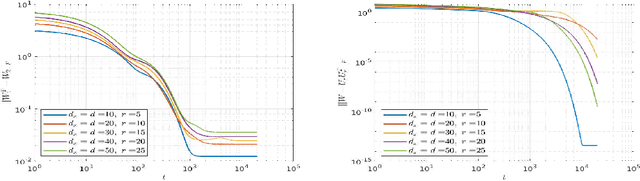
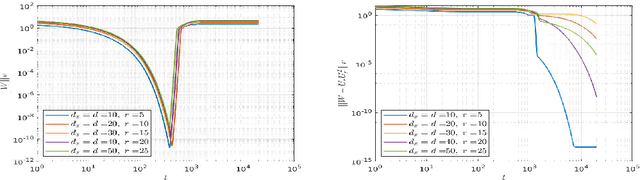
We study the convergence of gradient flows related to learning deep linear neural networks from data (i.e., the activation function is the identity map). In this case, the composition of the network layers amounts to simply multiplying the weight matrices of all layers together, resulting in an overparameterized problem. We show that the gradient flow with respect to these factors can be re-interpreted as a Riemannian gradient flow on the manifold of rank-$r$ matrices endowed with a suitable Riemannian metric. We show that the flow always converges to a critical point of the underlying functional. Moreover, in the special case of an autoencoder, we show that the flow converges to a global minimum for almost all initializations.