Bayesian Hierarchical Probabilistic Forecasting of Intraday Electricity Prices

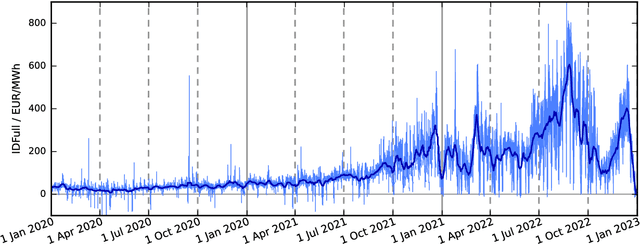
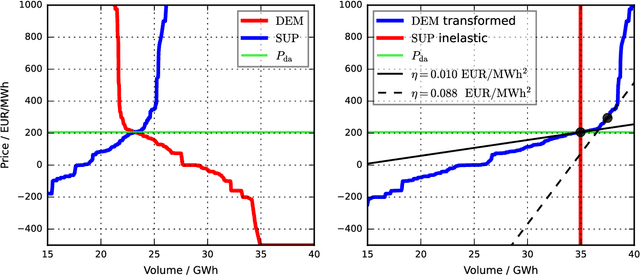
We present a first study of Bayesian forecasting of electricity prices traded on the German continuous intraday market which fully incorporates parameter uncertainty. Our target variable is the IDFull price index, forecasts are given in terms of posterior predictive distributions. For validation we use the exceedingly volatile electricity prices of 2022, which have hardly been the subject of forecasting studies before. As a benchmark model, we use all available intraday transactions at the time of forecast creation to compute a current value for the IDFull. According to the weak-form efficiency hypothesis, it would not be possible to significantly improve this benchmark built from last price information. We do, however, observe statistically significant improvement in terms of both point measures and probability scores. Finally, we challenge the declared gold standard of using LASSO for feature selection in electricity price forecasting by presenting strong statistical evidence that Orthogonal Matching Pursuit (OMP) leads to better forecasting performance.

Improved identification accuracy in equation learning via comprehensive $\boldsymbol{R^2}$-elimination and Bayesian model selection

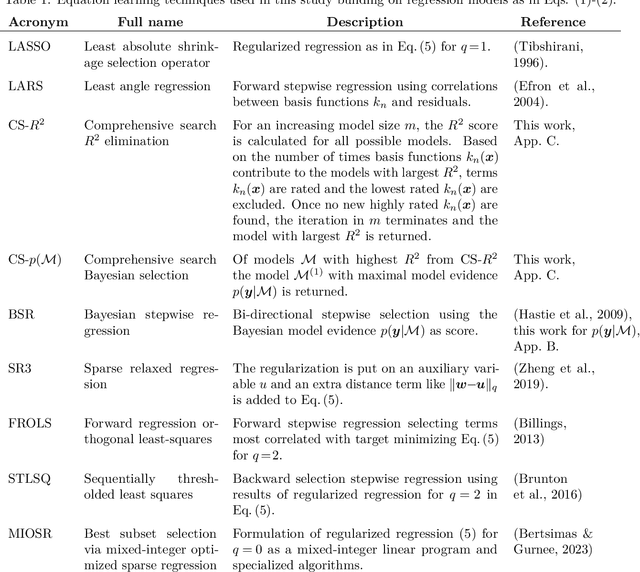
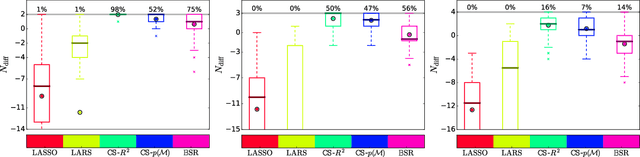
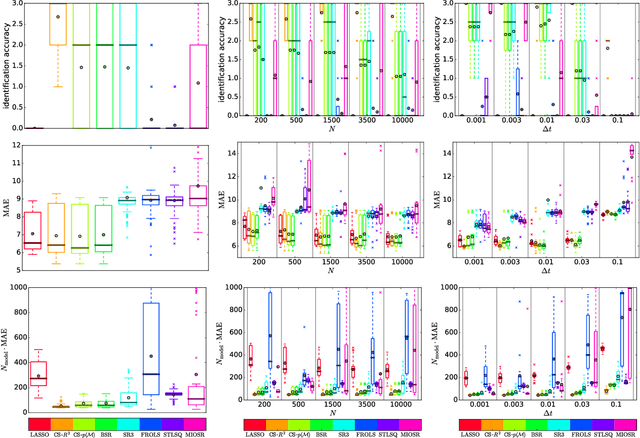
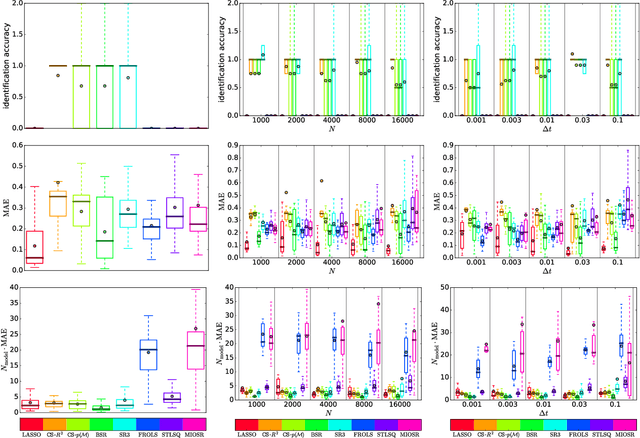
In the field of equation learning, exhaustively considering all possible equations derived from a basis function dictionary is infeasible. Sparse regression and greedy algorithms have emerged as popular approaches to tackle this challenge. However, the presence of multicollinearity poses difficulties for sparse regression techniques, and greedy steps may inadvertently exclude terms of the true equation, leading to reduced identification accuracy. In this article, we present an approach that strikes a balance between comprehensiveness and efficiency in equation learning. Inspired by stepwise regression, our approach combines the coefficient of determination, $R^2$, and the Bayesian model evidence, $p(\boldsymbol y|\mathcal M)$, in a novel way. Our procedure is characterized by a comprehensive search with just a minor reduction of the model space at each iteration step. With two flavors of our approach and the adoption of $p(\boldsymbol y|\mathcal M)$ for bi-directional stepwise regression, we present a total of three new avenues for equation learning. Through three extensive numerical experiments involving random polynomials and dynamical systems, we compare our approach against four state-of-the-art methods and two standard approaches. The results demonstrate that our comprehensive search approach surpasses all other methods in terms of identification accuracy. In particular, the second flavor of our approach establishes an efficient overfitting penalty solely based on $R^2$, which achieves highest rates of exact equation recovery.