Birol Yuceoglu
Rule Covering for Interpretation and Boosting
Jul 13, 2020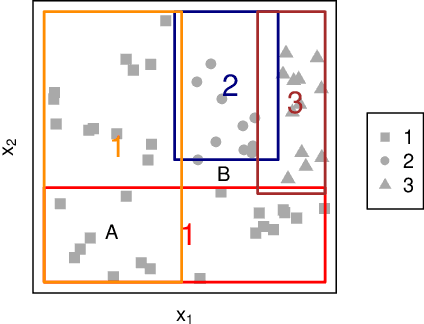
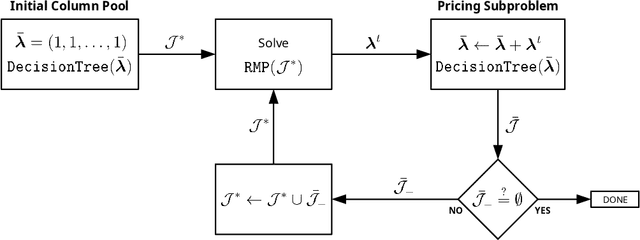
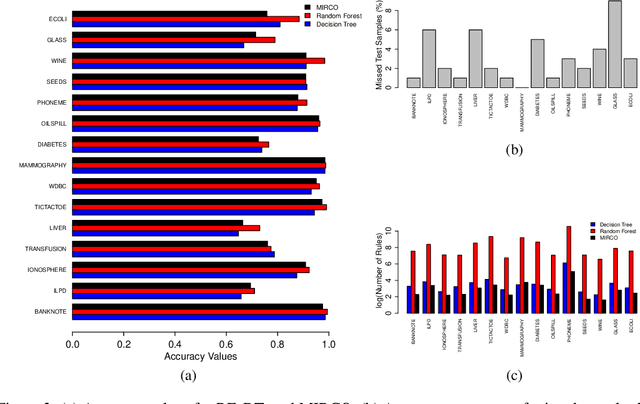
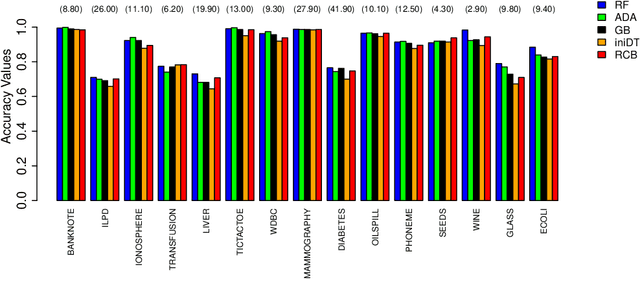
Abstract:We propose two algorithms for interpretation and boosting of tree-based ensemble methods. Both algorithms make use of mathematical programming models that are constructed with a set of rules extracted from an ensemble of decision trees. The objective is to obtain the minimum total impurity with the least number of rules that cover all the samples. The first algorithm uses the collection of decision trees obtained from a trained random forest model. Our numerical results show that the proposed rule covering approach selects only a few rules that could be used for interpreting the random forest model. Moreover, the resulting set of rules closely matches the accuracy level of the random forest model. Inspired by the column generation algorithm in linear programming, our second algorithm uses a rule generation scheme for boosting decision trees. We use the dual optimal solutions of the linear programming models as sample weights to obtain only those rules that would improve the accuracy. With a computational study, we observe that our second algorithm performs competitively with the other well-known boosting methods. Our implementations also demonstrate that both algorithms can be trivially coupled with the existing random forest and decision tree packages.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge