High-Dimensional Bayesian Structure Learning in Gaussian Graphical Models using Marginal Pseudo-Likelihood

Gaussian graphical models depict the conditional dependencies between variables within a multivariate normal distribution in a graphical format. The identification of these graph structures is an area known as structure learning. However, when utilizing Bayesian methodologies in structure learning, computational complexities can arise, especially with high-dimensional graphs surpassing 250 nodes. This paper introduces two innovative search algorithms that employ marginal pseudo-likelihood to address this computational challenge. These methods can swiftly generate reliable estimations for problems encompassing 1000 variables in just a few minutes on standard computers. For those interested in practical applications, the code supporting this new approach is made available through the R package BDgraph.

Continuous-Time Birth-Death MCMC for Bayesian Regression Tree Models

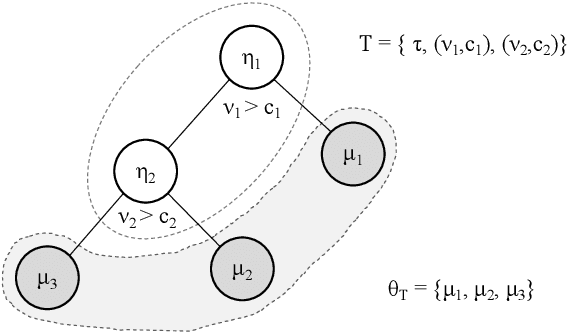
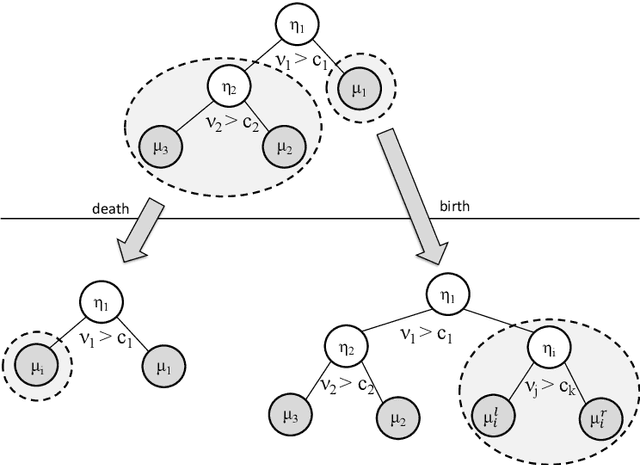
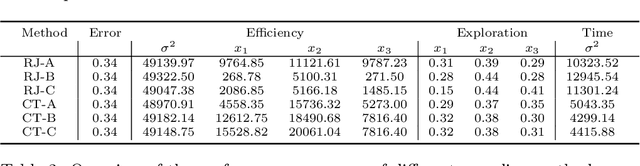
Decision trees are flexible models that are well suited for many statistical regression problems. In a Bayesian framework for regression trees, Markov Chain Monte Carlo (MCMC) search algorithms are required to generate samples of tree models according to their posterior probabilities. The critical component of such an MCMC algorithm is to construct good Metropolis-Hastings steps for updating the tree topology. However, such algorithms frequently suffering from local mode stickiness and poor mixing. As a result, the algorithms are slow to converge. Hitherto, authors have primarily used discrete-time birth/death mechanisms for Bayesian (sums of) regression tree models to explore the model space. These algorithms are efficient only if the acceptance rate is high which is not always the case. Here we overcome this issue by developing a new search algorithm which is based on a continuous-time birth-death Markov process. This search algorithm explores the model space by jumping between parameter spaces corresponding to different tree structures. In the proposed algorithm, the moves between models are always accepted which can dramatically improve the convergence and mixing properties of the MCMC algorithm. We provide theoretical support of the algorithm for Bayesian regression tree models and demonstrate its performance.

The ratio of normalizing constants for Bayesian graphical Gaussian model selection

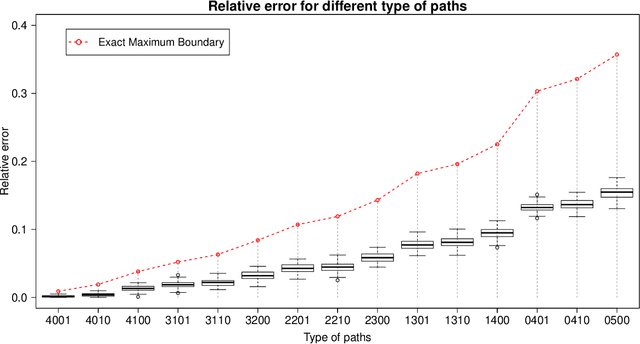
Many graphical Gaussian selection methods in a Bayesian framework use the G-Wishart as the conjugate prior on the precision matrix. The Bayes factor to compare a model governed by a graph G and a model governed by the neighboring graph G-e, derived from G by deleting an edge e, is a function of the ratios of prior and posterior normalizing constants of the G-Wishart for G and G-e. While more recent methods avoid the computation of the posterior ratio, computing the ratio of prior normalizing constants, (2) below, has remained a computational stumbling block. In this paper, we propose an explicit analytic approximation to (2) which is equal to the ratio of two Gamma functions evaluated at (delta+d)/2 and (delta+d+1)/2 respectively, where delta is the shape parameter of the G-Wishart and d is the number of paths of length two between the endpoints of e. This approximation allows us to avoid Monte Carlo methods, is computationally inexpensive and is scalable to high-dimensional problems. We show that the ratio of the approximation to the true value is always between zero and one and so, one cannot incur wild errors. In the particular case where the paths between the endpoints of e are disjoint, we show that the approximation is very good. When the paths between these two endpoints are not disjoint we give a sufficient condition for the approximation to be good. Numerical results show that the ratio of the approximation to the true value of the prior ratio is always between .55 and 1 and very often close to 1. We compare the results obtained with a model search using our approximation and a search using the double Metropolis-Hastings algorithm to compute the prior ratio. The results are extremely close.