Rethinking Knowledge Transfer in Learning Using Privileged Information

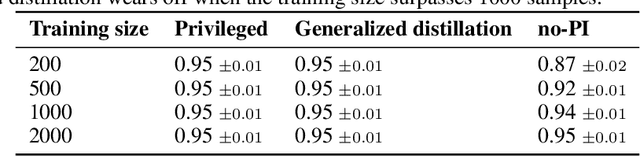
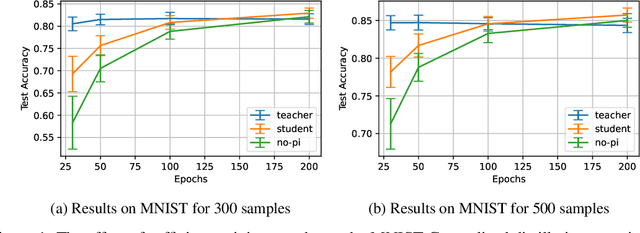
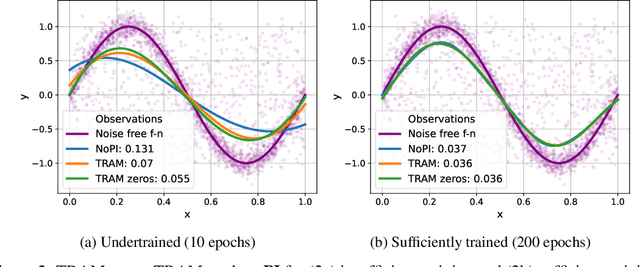
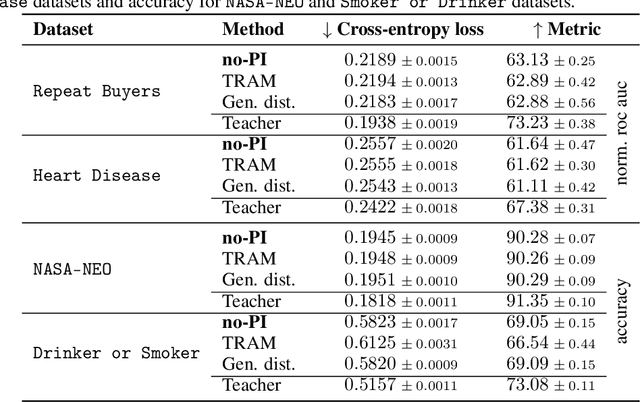
In supervised machine learning, privileged information (PI) is information that is unavailable at inference, but is accessible during training time. Research on learning using privileged information (LUPI) aims to transfer the knowledge captured in PI onto a model that can perform inference without PI. It seems that this extra bit of information ought to make the resulting model better. However, finding conclusive theoretical or empirical evidence that supports the ability to transfer knowledge using PI has been challenging. In this paper, we critically examine the assumptions underlying existing theoretical analyses and argue that there is little theoretical justification for when LUPI should work. We analyze LUPI methods and reveal that apparent improvements in empirical risk of existing research may not directly result from PI. Instead, these improvements often stem from dataset anomalies or modifications in model design misguidedly attributed to PI. Our experiments for a wide variety of application domains further demonstrate that state-of-the-art LUPI approaches fail to effectively transfer knowledge from PI. Thus, we advocate for practitioners to exercise caution when working with PI to avoid unintended inductive biases.

Efficient Exploration in Average-Reward Constrained Reinforcement Learning: Achieving Near-Optimal Regret With Posterior Sampling

We present a new algorithm based on posterior sampling for learning in Constrained Markov Decision Processes (CMDP) in the infinite-horizon undiscounted setting. The algorithm achieves near-optimal regret bounds while being advantageous empirically compared to the existing algorithms. Our main theoretical result is a Bayesian regret bound for each cost component of $\tilde{O} (DS\sqrt{AT})$ for any communicating CMDP with $S$ states, $A$ actions, and diameter $D$. This regret bound matches the lower bound in order of time horizon $T$ and is the best-known regret bound for communicating CMDPs achieved by a computationally tractable algorithm. Empirical results show that our posterior sampling algorithm outperforms the existing algorithms for constrained reinforcement learning.

Provably Efficient Exploration in Constrained Reinforcement Learning:Posterior Sampling Is All You Need

We present a new algorithm based on posterior sampling for learning in constrained Markov decision processes (CMDP) in the infinite-horizon undiscounted setting. The algorithm achieves near-optimal regret bounds while being advantageous empirically compared to the existing algorithms. Our main theoretical result is a Bayesian regret bound for each cost component of \tilde{O} (HS \sqrt{AT}) for any communicating CMDP with S states, A actions, and bound on the hitting time H. This regret bound matches the lower bound in order of time horizon T and is the best-known regret bound for communicating CMDPs in the infinite-horizon undiscounted setting. Empirical results show that, despite its simplicity, our posterior sampling algorithm outperforms the existing algorithms for constrained reinforcement learning.

An Empirical Evaluation of Posterior Sampling for Constrained Reinforcement Learning

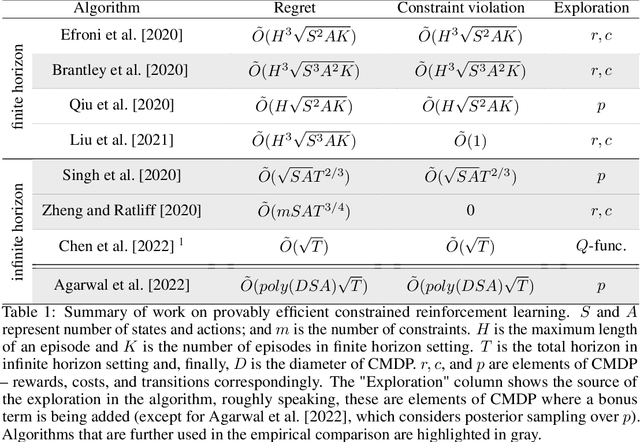
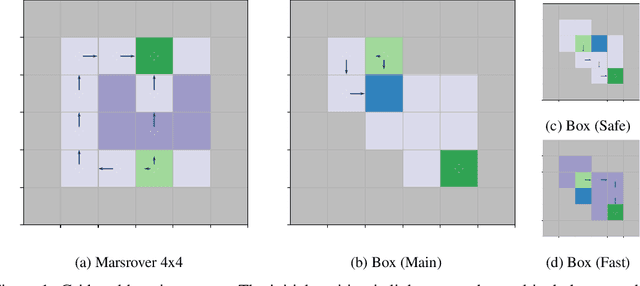
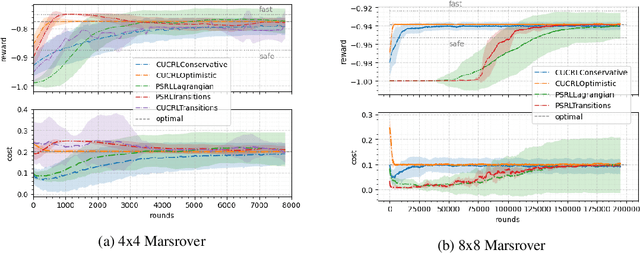
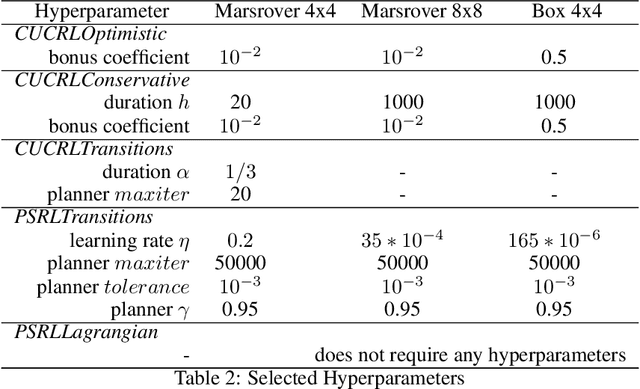
We study a posterior sampling approach to efficient exploration in constrained reinforcement learning. Alternatively to existing algorithms, we propose two simple algorithms that are more efficient statistically, simpler to implement and computationally cheaper. The first algorithm is based on a linear formulation of CMDP, and the second algorithm leverages the saddle-point formulation of CMDP. Our empirical results demonstrate that, despite its simplicity, posterior sampling achieves state-of-the-art performance and, in some cases, significantly outperforms optimistic algorithms.

The Impact of Batch Learning in Stochastic Linear Bandits

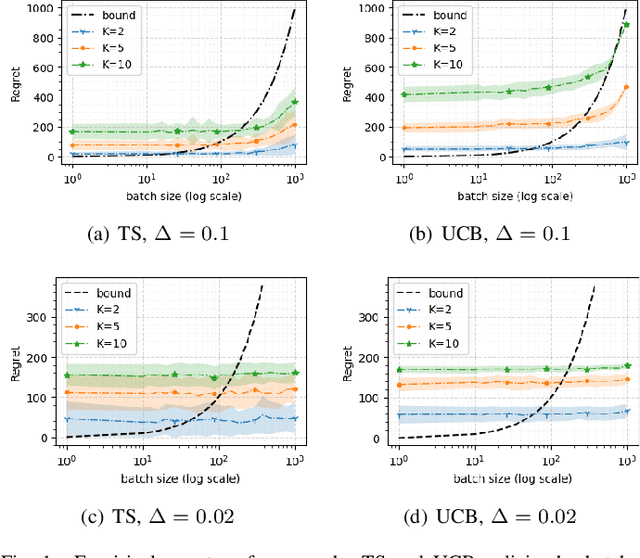
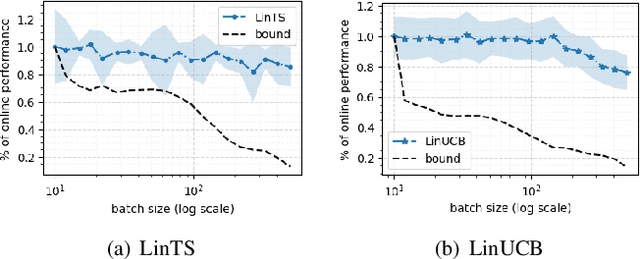
We consider a special case of bandit problems, named batched bandits, in which an agent observes batches of responses over a certain time period. Unlike previous work, we consider a practically relevant batch-centric scenario of batch learning. That is to say, we provide a policy-agnostic regret analysis and demonstrate upper and lower bounds for the regret of a candidate policy. Our main theoretical results show that the impact of batch learning can be measured proportional to the regret of online behavior. Primarily, we study two settings of the problem: instance-independent and instance-dependent. While the upper bound is the same for both settings, the worst-case lower bound is more comprehensive in the former case and more accurate in the latter one. Also, we provide a more robust result for the 2-armed bandit problem as an important insight. Finally, we demonstrate the consistency of theoretical results by conducting empirical experiments and reflect on the optimal batch size choice.

The Impact of Batch Learning in Stochastic Bandits

We consider a special case of bandit problems, namely batched bandits. Motivated by natural restrictions of recommender systems and e-commerce platforms, we assume that a learning agent observes responses batched in groups over a certain time period. Unlike previous work, we consider a more practically relevant batch-centric scenario of batch learning. We provide a policy-agnostic regret analysis and demonstrate upper and lower bounds for the regret of a candidate policy. Our main theoretical results show that the impact of batch learning can be measured in terms of online behavior. Finally, we demonstrate the consistency of theoretical results by conducting empirical experiments and reflect on the optimal batch size choice.

Exploring Offline Policy Evaluation for the Continuous-Armed Bandit Problem

The (contextual) multi-armed bandit problem (MAB) provides a formalization of sequential decision-making which has many applications. However, validly evaluating MAB policies is challenging; we either resort to simulations which inherently include debatable assumptions, or we resort to expensive field trials. Recently an offline evaluation method has been suggested that is based on empirical data, thus relaxing the assumptions, and can be used to evaluate multiple competing policies in parallel. This method is however not directly suited for the continuous armed (CAB) problem; an often encountered version of the MAB problem in which the action set is continuous instead of discrete. We propose and evaluate an extension of the existing method such that it can be used to evaluate CAB policies. We empirically demonstrate that our method provides a relatively consistent ranking of policies. Furthermore, we detail how our method can be used to select policies in a real-life CAB problem.

Continuous-Time Birth-Death MCMC for Bayesian Regression Tree Models

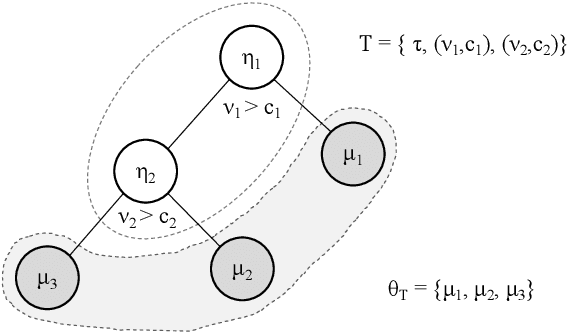
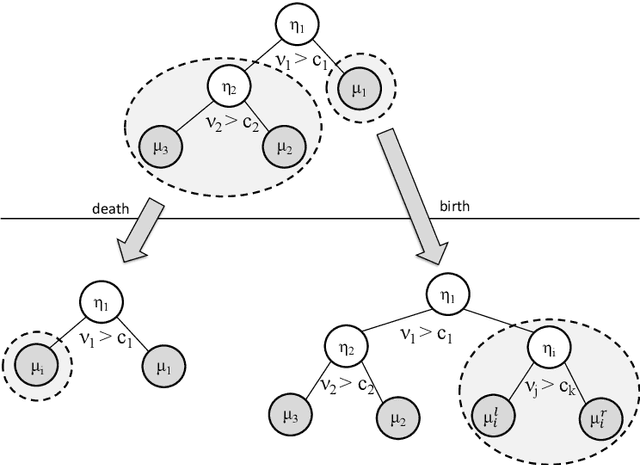
Decision trees are flexible models that are well suited for many statistical regression problems. In a Bayesian framework for regression trees, Markov Chain Monte Carlo (MCMC) search algorithms are required to generate samples of tree models according to their posterior probabilities. The critical component of such an MCMC algorithm is to construct good Metropolis-Hastings steps for updating the tree topology. However, such algorithms frequently suffering from local mode stickiness and poor mixing. As a result, the algorithms are slow to converge. Hitherto, authors have primarily used discrete-time birth/death mechanisms for Bayesian (sums of) regression tree models to explore the model space. These algorithms are efficient only if the acceptance rate is high which is not always the case. Here we overcome this issue by developing a new search algorithm which is based on a continuous-time birth-death Markov process. This search algorithm explores the model space by jumping between parameter spaces corresponding to different tree structures. In the proposed algorithm, the moves between models are always accepted which can dramatically improve the convergence and mixing properties of the MCMC algorithm. We provide theoretical support of the algorithm for Bayesian regression tree models and demonstrate its performance.

contextual: Evaluating Contextual Multi-Armed Bandit Problems in R

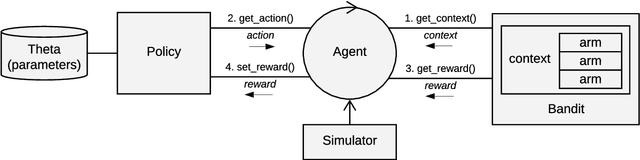
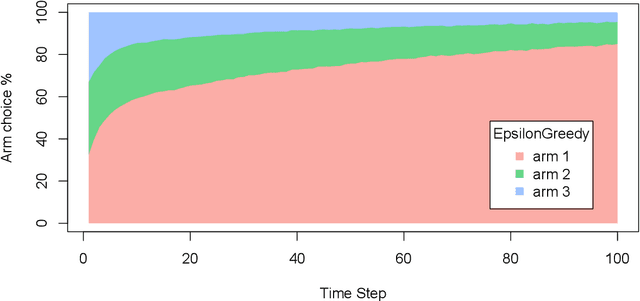
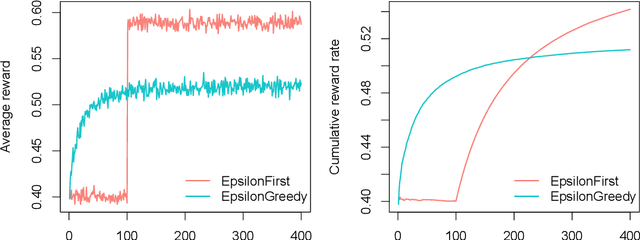
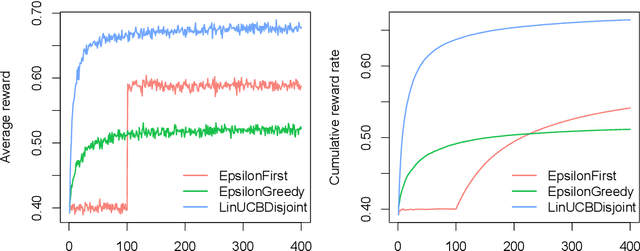
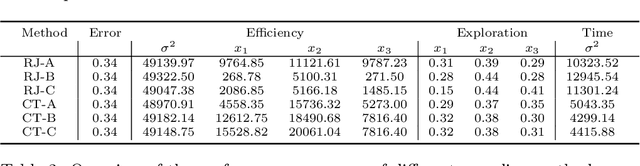
Over the past decade, contextual bandit algorithms have been gaining in popularity due to their effectiveness and flexibility in solving sequential decision problems---from online advertising and finance to clinical trial design and personalized medicine. At the same time, there are, as of yet, surprisingly few options that enable researchers and practitioners to simulate and compare the wealth of new and existing bandit algorithms in a standardized way. To help close this gap between analytical research and empirical evaluation the current paper introduces the object-oriented R package "contextual": a user-friendly and, through its object-oriented structure, easily extensible framework that facilitates parallelized comparison of contextual and context-free bandit policies through both simulation and offline analysis.

Maximum likelihood estimation of a finite mixture of logistic regression models in a continuous data stream

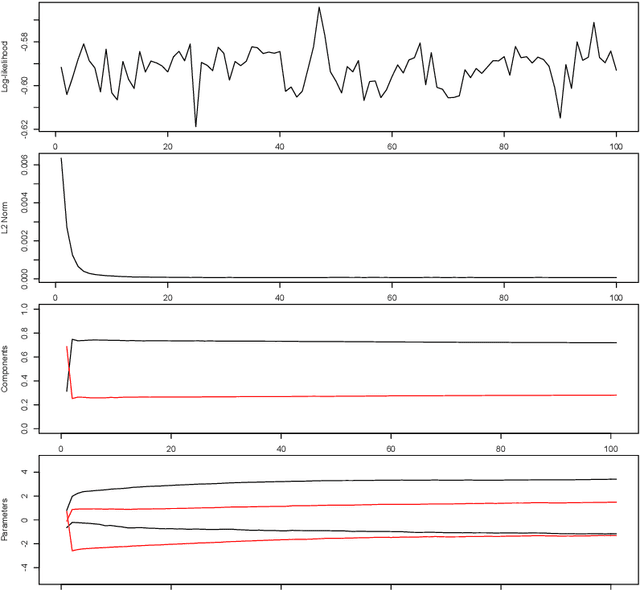
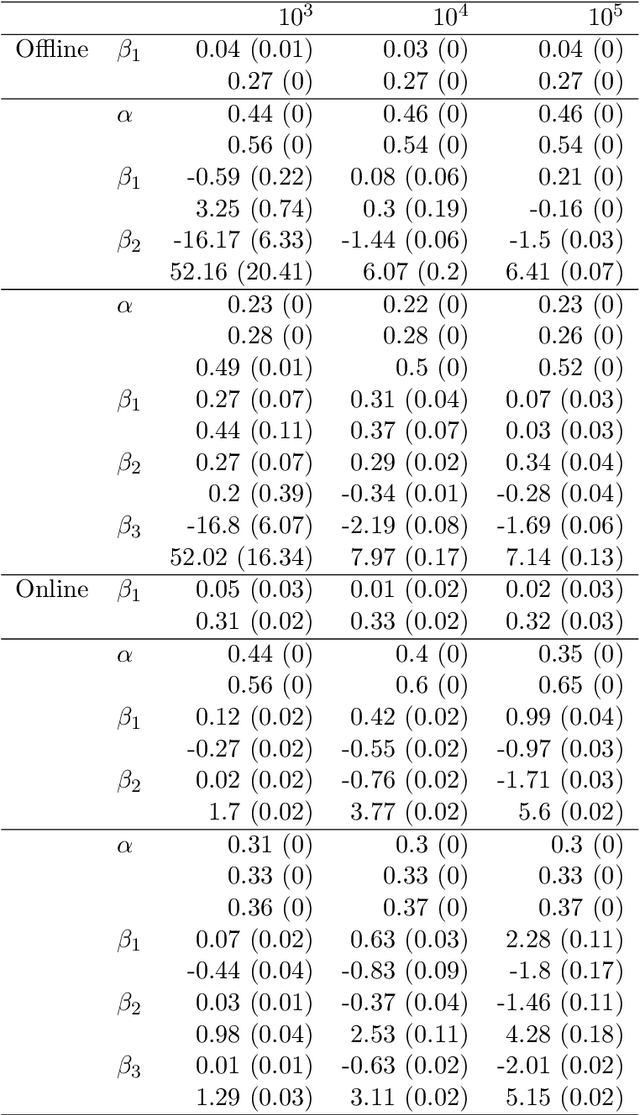
In marketing we are often confronted with a continuous stream of responses to marketing messages. Such streaming data provide invaluable information regarding message effectiveness and segmentation. However, streaming data are hard to analyze using conventional methods: their high volume and the fact that they are continuously augmented means that it takes considerable time to analyze them. We propose a method for estimating a finite mixture of logistic regression models which can be used to cluster customers based on a continuous stream of responses. This method, which we coin oFMLR, allows segments to be identified in data streams or extremely large static datasets. Contrary to black box algorithms, oFMLR provides model estimates that are directly interpretable. We first introduce oFMLR, explaining in passing general topics such as online estimation and the EM algorithm, making this paper a high level overview of possible methods of dealing with large data streams in marketing practice. Next, we discuss model convergence, identifiability, and relations to alternative, Bayesian, methods; we also identify more general issues that arise from dealing with continuously augmented data sets. Finally, we introduce the oFMLR [R] package and evaluate the method by numerical simulation and by analyzing a large customer clickstream dataset.