Rethinking Knowledge Transfer in Learning Using Privileged Information

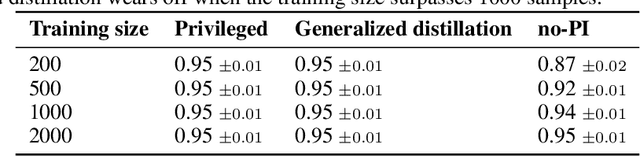
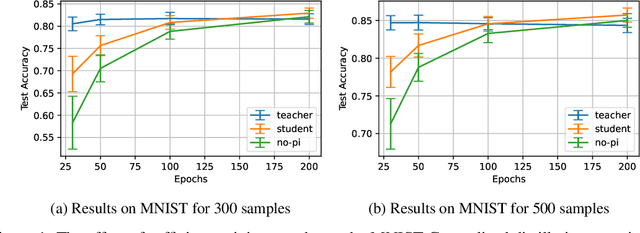
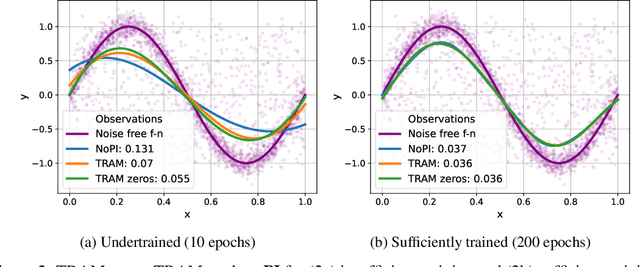
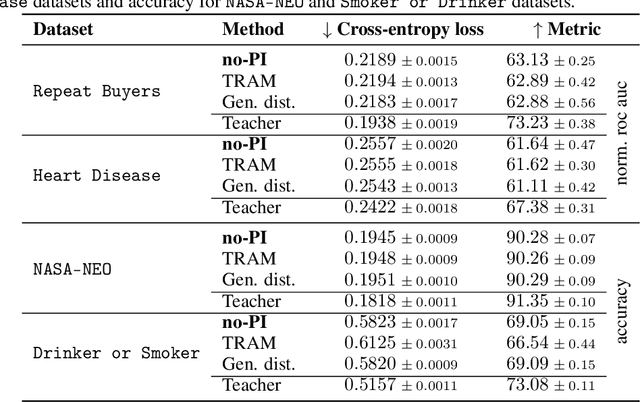
In supervised machine learning, privileged information (PI) is information that is unavailable at inference, but is accessible during training time. Research on learning using privileged information (LUPI) aims to transfer the knowledge captured in PI onto a model that can perform inference without PI. It seems that this extra bit of information ought to make the resulting model better. However, finding conclusive theoretical or empirical evidence that supports the ability to transfer knowledge using PI has been challenging. In this paper, we critically examine the assumptions underlying existing theoretical analyses and argue that there is little theoretical justification for when LUPI should work. We analyze LUPI methods and reveal that apparent improvements in empirical risk of existing research may not directly result from PI. Instead, these improvements often stem from dataset anomalies or modifications in model design misguidedly attributed to PI. Our experiments for a wide variety of application domains further demonstrate that state-of-the-art LUPI approaches fail to effectively transfer knowledge from PI. Thus, we advocate for practitioners to exercise caution when working with PI to avoid unintended inductive biases.

Efficient Exploration in Average-Reward Constrained Reinforcement Learning: Achieving Near-Optimal Regret With Posterior Sampling

We present a new algorithm based on posterior sampling for learning in Constrained Markov Decision Processes (CMDP) in the infinite-horizon undiscounted setting. The algorithm achieves near-optimal regret bounds while being advantageous empirically compared to the existing algorithms. Our main theoretical result is a Bayesian regret bound for each cost component of $\tilde{O} (DS\sqrt{AT})$ for any communicating CMDP with $S$ states, $A$ actions, and diameter $D$. This regret bound matches the lower bound in order of time horizon $T$ and is the best-known regret bound for communicating CMDPs achieved by a computationally tractable algorithm. Empirical results show that our posterior sampling algorithm outperforms the existing algorithms for constrained reinforcement learning.

Provably Efficient Exploration in Constrained Reinforcement Learning:Posterior Sampling Is All You Need

We present a new algorithm based on posterior sampling for learning in constrained Markov decision processes (CMDP) in the infinite-horizon undiscounted setting. The algorithm achieves near-optimal regret bounds while being advantageous empirically compared to the existing algorithms. Our main theoretical result is a Bayesian regret bound for each cost component of \tilde{O} (HS \sqrt{AT}) for any communicating CMDP with S states, A actions, and bound on the hitting time H. This regret bound matches the lower bound in order of time horizon T and is the best-known regret bound for communicating CMDPs in the infinite-horizon undiscounted setting. Empirical results show that, despite its simplicity, our posterior sampling algorithm outperforms the existing algorithms for constrained reinforcement learning.

Learning Optimal Bidding Strategy: Case Study in E-Commerce Advertising

Although the bandits framework is a classical and well-suited approach for optimal bidding strategies in sponsored search auctions, industrial attempts are rarely documented. This paper outlines the development process at Zalando, a leading fashion e-commerce company, and describes the promising outcomes of a bandits-based approach to increase profitability in sponsored search auctions. We discuss in detail the technical and theoretical challenges that were overcome during the implementation, as well as the mechanisms that led to increased profitability.

An Empirical Evaluation of Posterior Sampling for Constrained Reinforcement Learning

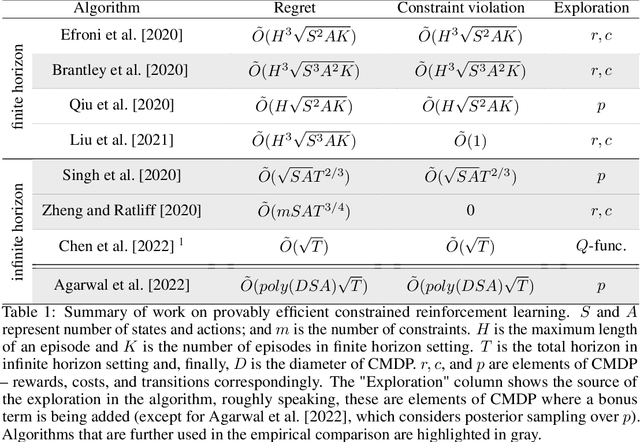
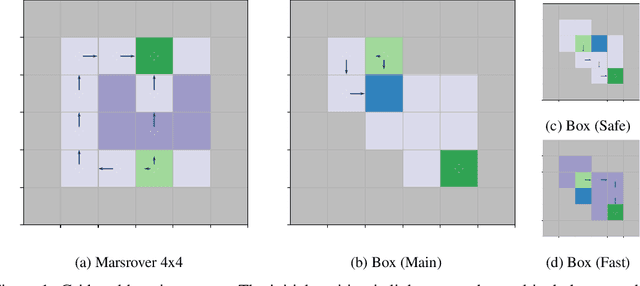
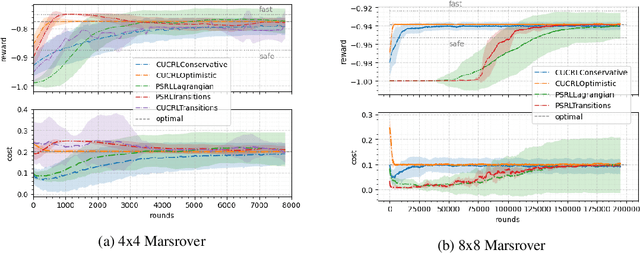
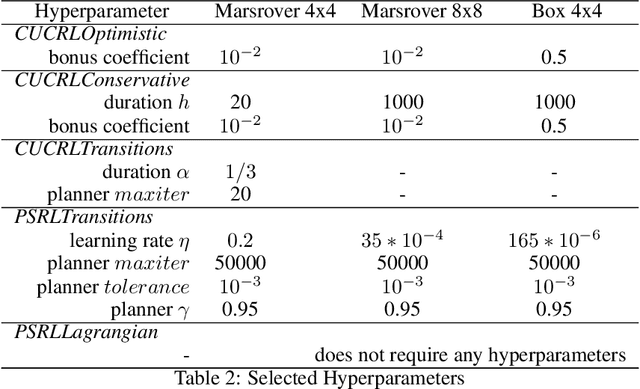
We study a posterior sampling approach to efficient exploration in constrained reinforcement learning. Alternatively to existing algorithms, we propose two simple algorithms that are more efficient statistically, simpler to implement and computationally cheaper. The first algorithm is based on a linear formulation of CMDP, and the second algorithm leverages the saddle-point formulation of CMDP. Our empirical results demonstrate that, despite its simplicity, posterior sampling achieves state-of-the-art performance and, in some cases, significantly outperforms optimistic algorithms.

The Impact of Batch Learning in Stochastic Linear Bandits

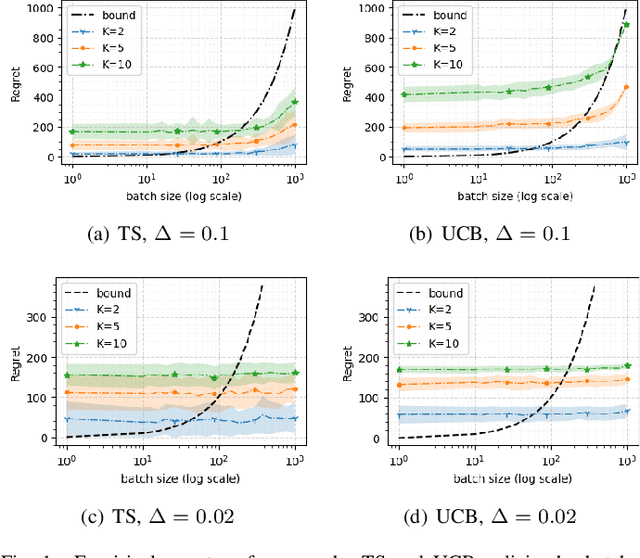
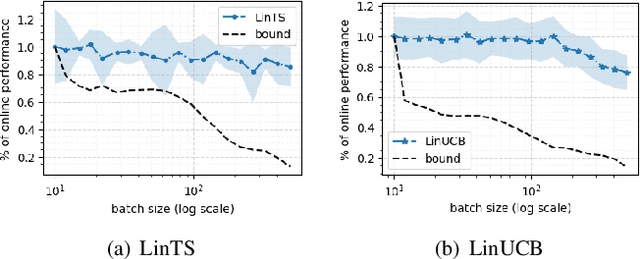
We consider a special case of bandit problems, named batched bandits, in which an agent observes batches of responses over a certain time period. Unlike previous work, we consider a practically relevant batch-centric scenario of batch learning. That is to say, we provide a policy-agnostic regret analysis and demonstrate upper and lower bounds for the regret of a candidate policy. Our main theoretical results show that the impact of batch learning can be measured proportional to the regret of online behavior. Primarily, we study two settings of the problem: instance-independent and instance-dependent. While the upper bound is the same for both settings, the worst-case lower bound is more comprehensive in the former case and more accurate in the latter one. Also, we provide a more robust result for the 2-armed bandit problem as an important insight. Finally, we demonstrate the consistency of theoretical results by conducting empirical experiments and reflect on the optimal batch size choice.

The Impact of Batch Learning in Stochastic Bandits

We consider a special case of bandit problems, namely batched bandits. Motivated by natural restrictions of recommender systems and e-commerce platforms, we assume that a learning agent observes responses batched in groups over a certain time period. Unlike previous work, we consider a more practically relevant batch-centric scenario of batch learning. We provide a policy-agnostic regret analysis and demonstrate upper and lower bounds for the regret of a candidate policy. Our main theoretical results show that the impact of batch learning can be measured in terms of online behavior. Finally, we demonstrate the consistency of theoretical results by conducting empirical experiments and reflect on the optimal batch size choice.