Rethinking Knowledge Transfer in Learning Using Privileged Information

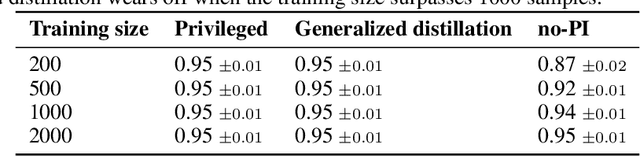
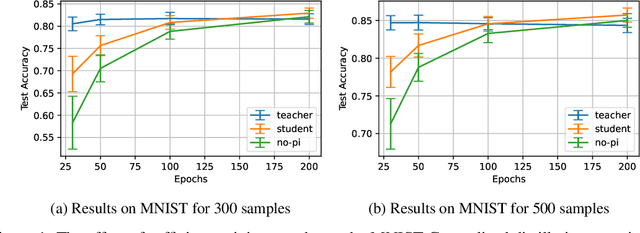
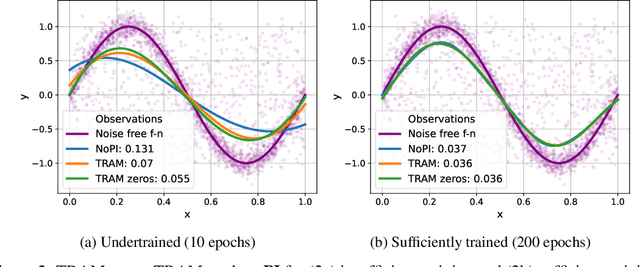
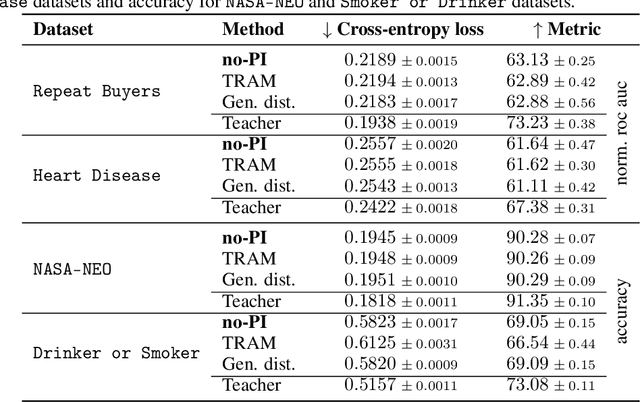
In supervised machine learning, privileged information (PI) is information that is unavailable at inference, but is accessible during training time. Research on learning using privileged information (LUPI) aims to transfer the knowledge captured in PI onto a model that can perform inference without PI. It seems that this extra bit of information ought to make the resulting model better. However, finding conclusive theoretical or empirical evidence that supports the ability to transfer knowledge using PI has been challenging. In this paper, we critically examine the assumptions underlying existing theoretical analyses and argue that there is little theoretical justification for when LUPI should work. We analyze LUPI methods and reveal that apparent improvements in empirical risk of existing research may not directly result from PI. Instead, these improvements often stem from dataset anomalies or modifications in model design misguidedly attributed to PI. Our experiments for a wide variety of application domains further demonstrate that state-of-the-art LUPI approaches fail to effectively transfer knowledge from PI. Thus, we advocate for practitioners to exercise caution when working with PI to avoid unintended inductive biases.

A/B/n Testing with Control in the Presence of Subpopulations

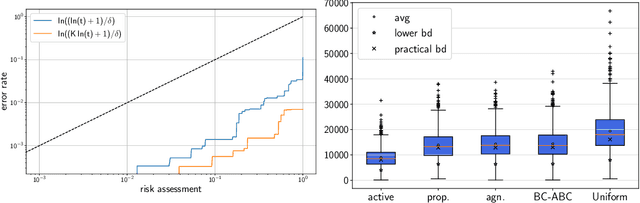
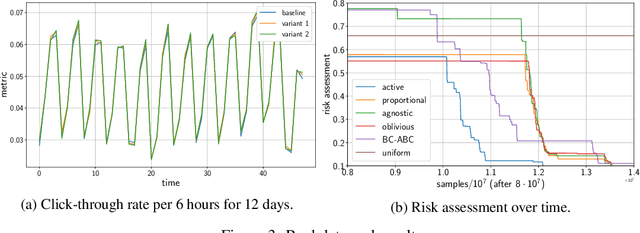
Motivated by A/B/n testing applications, we consider a finite set of distributions (called \emph{arms}), one of which is treated as a \emph{control}. We assume that the population is stratified into homogeneous subpopulations. At every time step, a subpopulation is sampled and an arm is chosen: the resulting observation is an independent draw from the arm conditioned on the subpopulation. The quality of each arm is assessed through a weighted combination of its subpopulation means. We propose a strategy for sequentially choosing one arm per time step so as to discover as fast as possible which arms, if any, have higher weighted expectation than the control. This strategy is shown to be asymptotically optimal in the following sense: if $\tau_\delta$ is the first time when the strategy ensures that it is able to output the correct answer with probability at least $1-\delta$, then $\mathbb{E}[\tau_\delta]$ grows linearly with $\log(1/\delta)$ at the exact optimal rate. This rate is identified in the paper in three different settings: (1) when the experimenter does not observe the subpopulation information, (2) when the subpopulation of each sample is observed but not chosen, and (3) when the experimenter can select the subpopulation from which each response is sampled. We illustrate the efficiency of the proposed strategy with numerical simulations on synthetic and real data collected from an A/B/n experiment.