The scalable Birth-Death MCMC Algorithm for Mixed Graphical Model Learning with Application to Genomic Data Integration

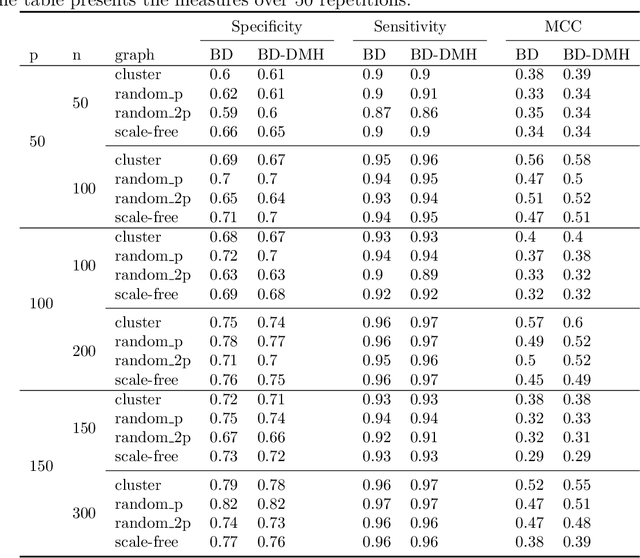
Recent advances in biological research have seen the emergence of high-throughput technologies with numerous applications that allow the study of biological mechanisms at an unprecedented depth and scale. A large amount of genomic data is now distributed through consortia like The Cancer Genome Atlas (TCGA), where specific types of biological information on specific type of tissue or cell are available. In cancer research, the challenge is now to perform integrative analyses of high-dimensional multi-omic data with the goal to better understand genomic processes that correlate with cancer outcomes, e.g. elucidate gene networks that discriminate a specific cancer subgroups (cancer sub-typing) or discovering gene networks that overlap across different cancer types (pan-cancer studies). In this paper, we propose a novel mixed graphical model approach to analyze multi-omic data of different types (continuous, discrete and count) and perform model selection by extending the Birth-Death MCMC (BDMCMC) algorithm initially proposed by \citet{stephens2000bayesian} and later developed by \cite{mohammadi2015bayesian}. We compare the performance of our method to the LASSO method and the standard BDMCMC method using simulations and find that our method is superior in terms of both computational efficiency and the accuracy of the model selection results. Finally, an application to the TCGA breast cancer data shows that integrating genomic information at different levels (mutation and expression data) leads to better subtyping of breast cancers.

The ratio of normalizing constants for Bayesian graphical Gaussian model selection

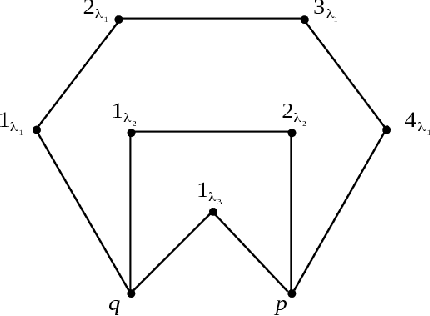
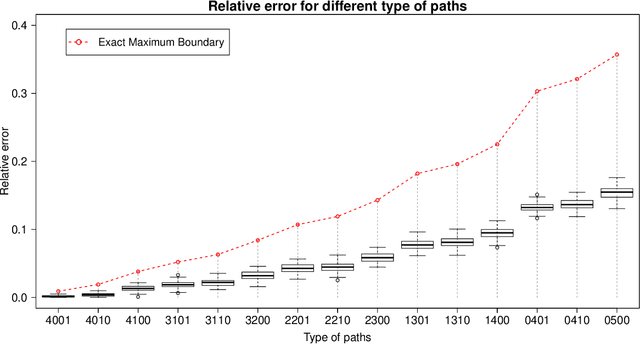
Many graphical Gaussian selection methods in a Bayesian framework use the G-Wishart as the conjugate prior on the precision matrix. The Bayes factor to compare a model governed by a graph G and a model governed by the neighboring graph G-e, derived from G by deleting an edge e, is a function of the ratios of prior and posterior normalizing constants of the G-Wishart for G and G-e. While more recent methods avoid the computation of the posterior ratio, computing the ratio of prior normalizing constants, (2) below, has remained a computational stumbling block. In this paper, we propose an explicit analytic approximation to (2) which is equal to the ratio of two Gamma functions evaluated at (delta+d)/2 and (delta+d+1)/2 respectively, where delta is the shape parameter of the G-Wishart and d is the number of paths of length two between the endpoints of e. This approximation allows us to avoid Monte Carlo methods, is computationally inexpensive and is scalable to high-dimensional problems. We show that the ratio of the approximation to the true value is always between zero and one and so, one cannot incur wild errors. In the particular case where the paths between the endpoints of e are disjoint, we show that the approximation is very good. When the paths between these two endpoints are not disjoint we give a sufficient condition for the approximation to be good. Numerical results show that the ratio of the approximation to the true value of the prior ratio is always between .55 and 1 and very often close to 1. We compare the results obtained with a model search using our approximation and a search using the double Metropolis-Hastings algorithm to compute the prior ratio. The results are extremely close.

A local approach to estimation in discrete loglinear models

We consider two connected aspects of maximum likelihood estimation of the parameter for high-dimensional discrete graphical models: the existence of the maximum likelihood estimate (mle) and its computation. When the data is sparse, there are many zeros in the contingency table and the maximum likelihood estimate of the parameter may not exist. Fienberg and Rinaldo (2012) have shown that the mle does not exists iff the data vector belongs to a face of the so-called marginal cone spanned by the rows of the design matrix of the model. Identifying these faces in high-dimension is challenging. In this paper, we take a local approach : we show that one such face, albeit possibly not the smallest one, can be identified by looking at a collection of marginal graphical models generated by induced subgraphs $G_i,i=1,\ldots,k$ of $G$. This is our first contribution. Our second contribution concerns the composite maximum likelihood estimate. When the dimension of the problem is large, estimating the parameters of a given graphical model through maximum likelihood is challenging, if not impossible. The traditional approach to this problem has been local with the use of composite likelihood based on local conditional likelihoods. A more recent development is to have the components of the composite likelihood be marginal likelihoods centred around each $v$. We first show that the estimates obtained by consensus through local conditional and marginal likelihoods are identical. We then study the asymptotic properties of the composite maximum likelihood estimate when both the dimension of the model and the sample size $N$ go to infinity.

Distributed parameter estimation of discrete hierarchical models via marginal likelihoods

We consider discrete graphical models Markov with respect to a graph $G$ and propose two distributed marginal methods to estimate the maximum likelihood estimate of the canonical parameter of the model. Both methods are based on a relaxation of the marginal likelihood obtained by considering the density of the variables represented by a vertex $v$ of $G$ and a neighborhood. The two methods differ by the size of the neighborhood of $v$. We show that the estimates are consistent and that those obtained with the larger neighborhood have smaller asymptotic variance than the ones obtained through the smaller neighborhood.