Differential Privacy of Noisy GD under Heavy-Tailed Perturbations

Injecting heavy-tailed noise to the iterates of stochastic gradient descent (SGD) has received increasing attention over the past few years. While various theoretical properties of the resulting algorithm have been analyzed mainly from learning theory and optimization perspectives, their privacy preservation properties have not yet been established. Aiming to bridge this gap, we provide differential privacy (DP) guarantees for noisy SGD, when the injected noise follows an $\alpha$-stable distribution, which includes a spectrum of heavy-tailed distributions (with infinite variance) as well as the Gaussian distribution. Considering the $(\epsilon, \delta)$-DP framework, we show that SGD with heavy-tailed perturbations achieves $(0, \tilde{\mathcal{O}}(1/n))$-DP for a broad class of loss functions which can be non-convex, where $n$ is the number of data points. As a remarkable byproduct, contrary to prior work that necessitates bounded sensitivity for the gradients or clipping the iterates, our theory reveals that under mild assumptions, such a projection step is not actually necessary. We illustrate that the heavy-tailed noising mechanism achieves similar DP guarantees compared to the Gaussian case, which suggests that it can be a viable alternative to its light-tailed counterparts.

Differentially Private Distributed Bayesian Linear Regression with MCMC

We propose a novel Bayesian inference framework for distributed differentially private linear regression. We consider a distributed setting where multiple parties hold parts of the data and share certain summary statistics of their portions in privacy-preserving noise. We develop a novel generative statistical model for privately shared statistics, which exploits a useful distributional relation between the summary statistics of linear regression. Bayesian estimation of the regression coefficients is conducted mainly using Markov chain Monte Carlo algorithms, while we also provide a fast version to perform Bayesian estimation in one iteration. The proposed methods have computational advantages over their competitors. We provide numerical results on both real and simulated data, which demonstrate that the proposed algorithms provide well-rounded estimation and prediction.

Differentially Private Online Bayesian Estimation With Adaptive Truncation

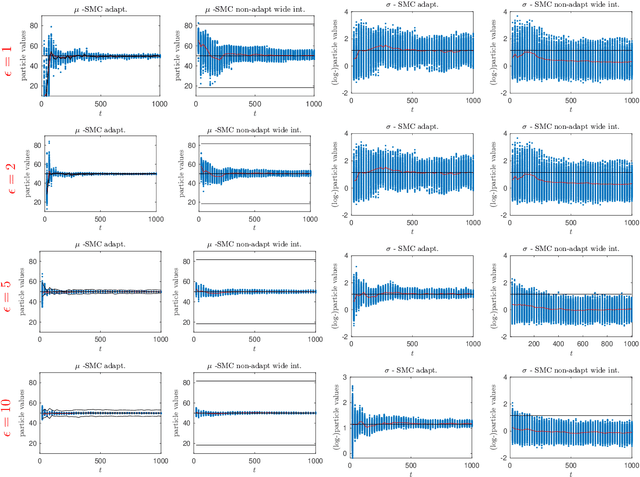
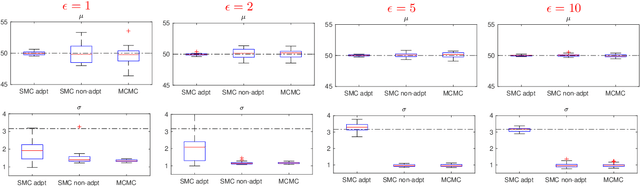
We propose a novel online and adaptive truncation method for differentially private Bayesian online estimation of a static parameter regarding a population. We assume that sensitive information from individuals is collected sequentially and the inferential aim is to estimate, on-the-fly, a static parameter regarding the population to which those individuals belong. We propose sequential Monte Carlo to perform online Bayesian estimation. When individuals provide sensitive information in response to a query, it is necessary to perturb it with privacy-preserving noise to ensure the privacy of those individuals. The amount of perturbation is proportional to the sensitivity of the query, which is determined usually by the range of the queried information. The truncation technique we propose adapts to the previously collected observations to adjust the query range for the next individual. The idea is that, based on previous observations, we can carefully arrange the interval into which the next individual's information is to be truncated before being perturbed with privacy-preserving noise. In this way, we aim to design predictive queries with small sensitivity, hence small privacy-preserving noise, enabling more accurate estimation while maintaining the same level of privacy. To decide on the location and the width of the interval, we use an exploration-exploitation approach a la Thompson sampling with an objective function based on the Fisher information of the generated observation. We show the merits of our methodology with numerical examples.

MCMC Shape Sampling for Image Segmentation with Nonparametric Shape Priors

Segmenting images of low quality or with missing data is a challenging problem. Integrating statistical prior information about the shapes to be segmented can improve the segmentation results significantly. Most shape-based segmentation algorithms optimize an energy functional and find a point estimate for the object to be segmented. This does not provide a measure of the degree of confidence in that result, neither does it provide a picture of other probable solutions based on the data and the priors. With a statistical view, addressing these issues would involve the problem of characterizing the posterior densities of the shapes of the objects to be segmented. For such characterization, we propose a Markov chain Monte Carlo (MCMC) sampling-based image segmentation algorithm that uses statistical shape priors. In addition to better characterization of the statistical structure of the problem, such an approach would also have the potential to address issues with getting stuck at local optima, suffered by existing shape-based segmentation methods. Our approach is able to characterize the posterior probability density in the space of shapes through its samples, and to return multiple solutions, potentially from different modes of a multimodal probability density, which would be encountered, e.g., in segmenting objects from multiple shape classes. We present promising results on a variety of data sets. We also provide an extension for segmenting shapes of objects with parts that can go through independent shape variations. This extension involves the use of local shape priors on object parts and provides robustness to limitations in shape training data size.

Bayesian tracking and parameter learning for non-linear multiple target tracking models

We propose a new Bayesian tracking and parameter learning algorithm for non-linear non-Gaussian multiple target tracking (MTT) models. We design a Markov chain Monte Carlo (MCMC) algorithm to sample from the posterior distribution of the target states, birth and death times, and association of observations to targets, which constitutes the solution to the tracking problem, as well as the model parameters. In the numerical section, we present performance comparisons with several competing techniques and demonstrate significant performance improvements in all cases.