Sumeetpal S. Singh
Bayesian learning of the optimal action-value function in a Markov decision process
May 03, 2025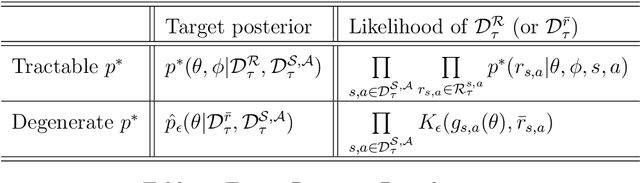
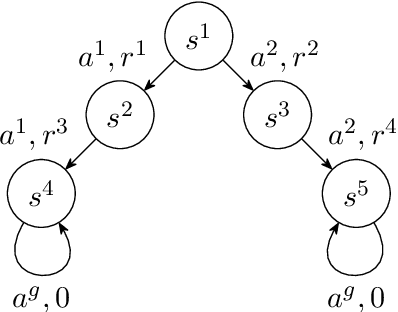

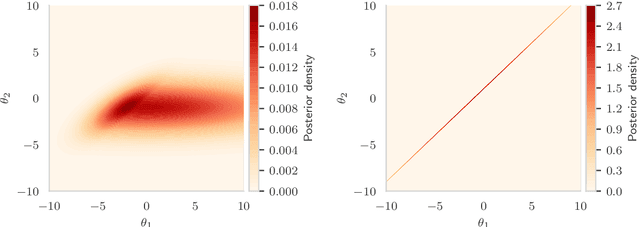
Abstract:The Markov Decision Process (MDP) is a popular framework for sequential decision-making problems, and uncertainty quantification is an essential component of it to learn optimal decision-making strategies. In particular, a Bayesian framework is used to maintain beliefs about the optimal decisions and the unknown ingredients of the model, which are also to be learned from the data, such as the rewards and state dynamics. However, many existing Bayesian approaches for learning the optimal decision-making strategy are based on unrealistic modelling assumptions and utilise approximate inference techniques. This raises doubts whether the benefits of Bayesian uncertainty quantification are fully realised or can be relied upon. We focus on infinite-horizon and undiscounted MDPs, with finite state and action spaces, and a terminal state. We provide a full Bayesian framework, from modelling to inference to decision-making. For modelling, we introduce a likelihood function with minimal assumptions for learning the optimal action-value function based on Bellman's optimality equations, analyse its properties, and clarify connections to existing works. For deterministic rewards, the likelihood is degenerate and we introduce artificial observation noise to relax it, in a controlled manner, to facilitate more efficient Monte Carlo-based inference. For inference, we propose an adaptive sequential Monte Carlo algorithm to both sample from and adjust the sequence of relaxed posterior distributions. For decision-making, we choose actions using samples from the posterior distribution over the optimal strategies. While commonly done, we provide new insight that clearly shows that it is a generalisation of Thompson sampling from multi-arm bandit problems. Finally, we evaluate our framework on the Deep Sea benchmark problem and demonstrate the exploration benefits of posterior sampling in MDPs.
Multilevel Bayesian Deep Neural Networks
Mar 29, 2022



Abstract:In this article we consider Bayesian inference associated to deep neural networks (DNNs) and in particular, trace-class neural network (TNN) priors which were proposed by Sell et al. [39]. Such priors were developed as more robust alternatives to classical architectures in the context of inference problems. For this work we develop multilevel Monte Carlo (MLMC) methods for such models. MLMC is a popular variance reduction technique, with particular applications in Bayesian statistics and uncertainty quantification. We show how a particular advanced MLMC method that was introduced in [4] can be applied to Bayesian inference from DNNs and establish mathematically, that the computational cost to achieve a particular mean square error, associated to posterior expectation computation, can be reduced by several orders, versus more conventional techniques. To verify such results we provide numerous numerical experiments on model problems arising in machine learning. These include Bayesian regression, as well as Bayesian classification and reinforcement learning.
Dimension-robust Function Space MCMC With Neural Network Priors
Dec 20, 2020



Abstract:This paper introduces a new prior on functions spaces which scales more favourably in the dimension of the function's domain compared to the usual Karhunen-Lo\'eve function space prior, a property we refer to as dimension-robustness. The proposed prior is a Bayesian neural network prior, where each weight and bias has an independent Gaussian prior, but with the key difference that the variances decrease in the width of the network, such that the variances form a summable sequence and the infinite width limit neural network is well defined. We show that our resulting posterior of the unknown function is amenable to sampling using Hilbert space Markov chain Monte Carlo methods. These sampling methods are favoured because they are stable under mesh-refinement, in the sense that the acceptance probability does not shrink to 0 as more parameters are introduced to better approximate the well-defined infinite limit. We show that our priors are competitive and have distinct advantages over other function space priors. Upon defining a suitable likelihood for continuous value functions in a Bayesian approach to reinforcement learning, our new prior is used in numerical examples to illustrate its performance and dimension-robustness.
Tracking multiple moving objects in images using Markov Chain Monte Carlo
Mar 17, 2016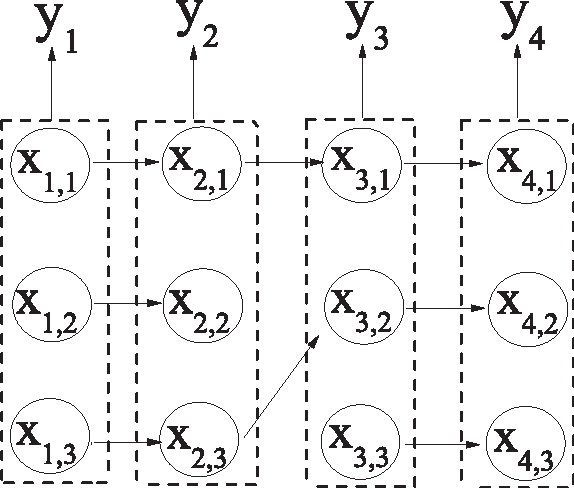
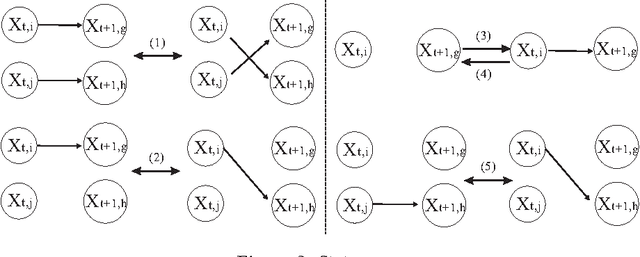
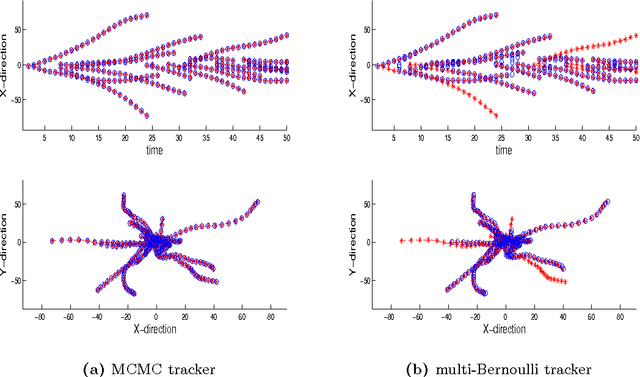

Abstract:A new Bayesian state and parameter learning algorithm for multiple target tracking (MTT) models with image observations is proposed. Specifically, a Markov chain Monte Carlo algorithm is designed to sample from the posterior distribution of the unknown number of targets, their birth and death times, states and model parameters, which constitutes the complete solution to the tracking problem. The conventional approach is to pre-process the images to extract point observations and then perform tracking. We model the image generation process directly to avoid potential loss of information when extracting point observations. Numerical examples show that our algorithm has improved tracking performance over commonly used techniques, for both synthetic examples and real florescent microscopy data, especially in the case of dim targets with overlapping illuminated regions.
Bayesian tracking and parameter learning for non-linear multiple target tracking models
Oct 08, 2014



Abstract:We propose a new Bayesian tracking and parameter learning algorithm for non-linear non-Gaussian multiple target tracking (MTT) models. We design a Markov chain Monte Carlo (MCMC) algorithm to sample from the posterior distribution of the target states, birth and death times, and association of observations to targets, which constitutes the solution to the tracking problem, as well as the model parameters. In the numerical section, we present performance comparisons with several competing techniques and demonstrate significant performance improvements in all cases.
An Online Expectation-Maximisation Algorithm for Nonnegative Matrix Factorisation Models
Jan 11, 2014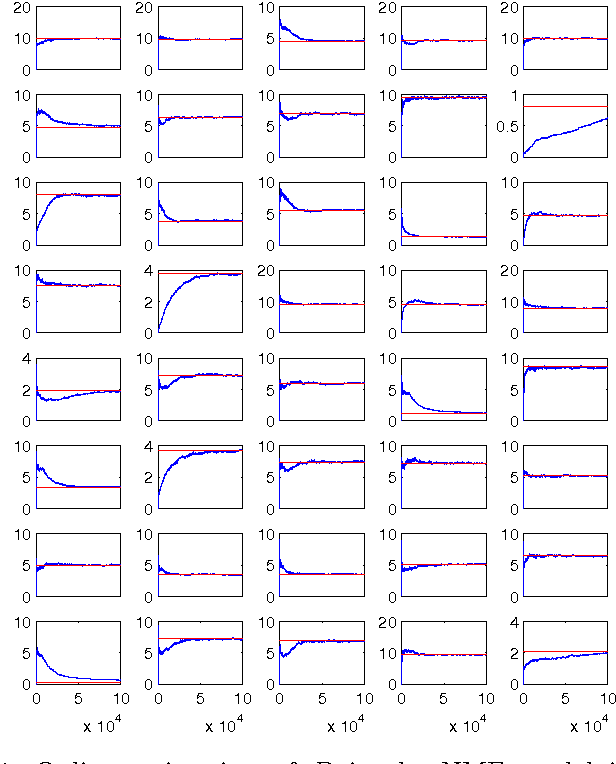
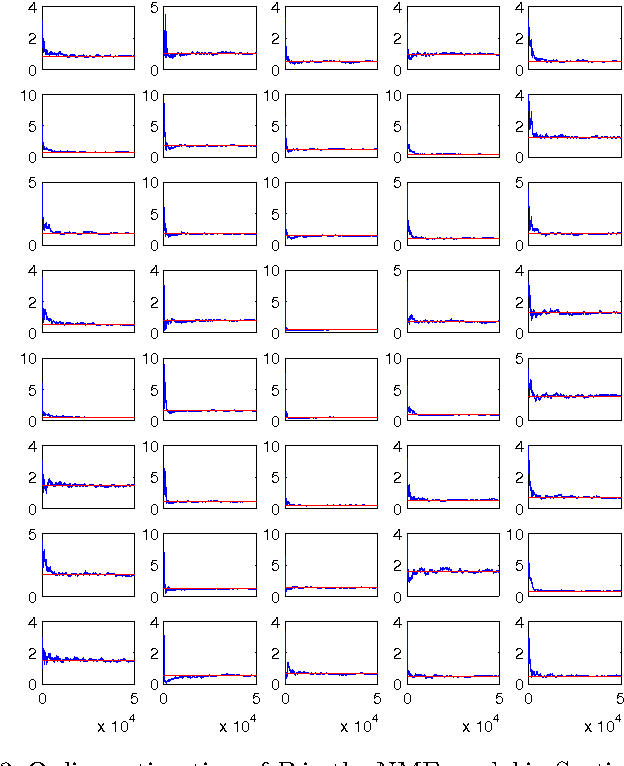
Abstract:In this paper we formulate the nonnegative matrix factorisation (NMF) problem as a maximum likelihood estimation problem for hidden Markov models and propose online expectation-maximisation (EM) algorithms to estimate the NMF and the other unknown static parameters. We also propose a sequential Monte Carlo approximation of our online EM algorithm. We show the performance of the proposed method with two numerical examples.
* 6 pages, 3 figures
Bayesian learning of noisy Markov decision processes
Nov 26, 2012



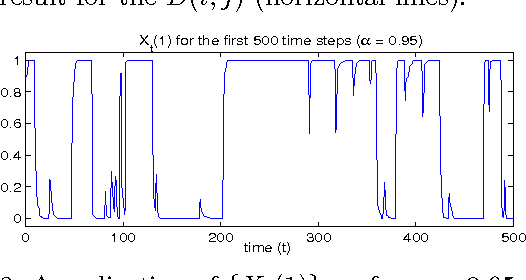
Abstract:We consider the inverse reinforcement learning problem, that is, the problem of learning from, and then predicting or mimicking a controller based on state/action data. We propose a statistical model for such data, derived from the structure of a Markov decision process. Adopting a Bayesian approach to inference, we show how latent variables of the model can be estimated, and how predictions about actions can be made, in a unified framework. A new Markov chain Monte Carlo (MCMC) sampler is devised for simulation from the posterior distribution. This step includes a parameter expansion step, which is shown to be essential for good convergence properties of the MCMC sampler. As an illustration, the method is applied to learning a human controller.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge