Differentially Private Online Bayesian Estimation With Adaptive Truncation
Paper and Code
Jan 19, 2023
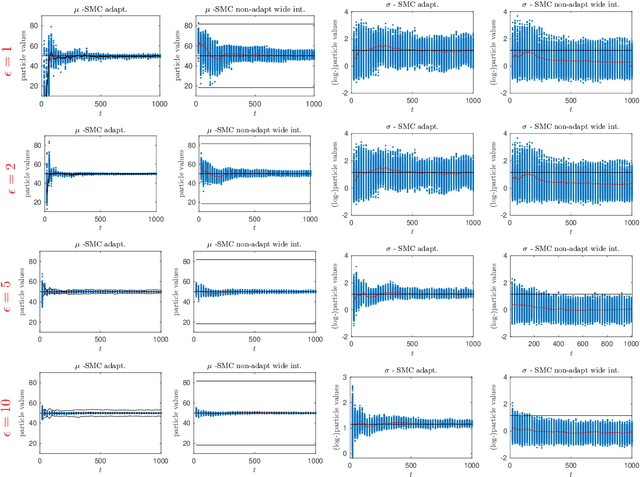
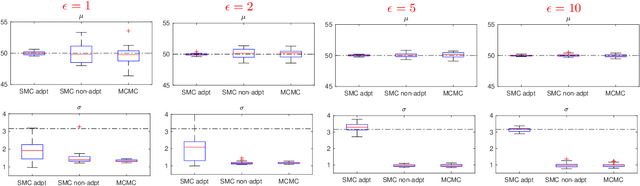
We propose a novel online and adaptive truncation method for differentially private Bayesian online estimation of a static parameter regarding a population. We assume that sensitive information from individuals is collected sequentially and the inferential aim is to estimate, on-the-fly, a static parameter regarding the population to which those individuals belong. We propose sequential Monte Carlo to perform online Bayesian estimation. When individuals provide sensitive information in response to a query, it is necessary to perturb it with privacy-preserving noise to ensure the privacy of those individuals. The amount of perturbation is proportional to the sensitivity of the query, which is determined usually by the range of the queried information. The truncation technique we propose adapts to the previously collected observations to adjust the query range for the next individual. The idea is that, based on previous observations, we can carefully arrange the interval into which the next individual's information is to be truncated before being perturbed with privacy-preserving noise. In this way, we aim to design predictive queries with small sensitivity, hence small privacy-preserving noise, enabling more accurate estimation while maintaining the same level of privacy. To decide on the location and the width of the interval, we use an exploration-exploitation approach a la Thompson sampling with an objective function based on the Fisher information of the generated observation. We show the merits of our methodology with numerical examples.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge