Stochastic Quasi-Newton Langevin Monte Carlo
Paper and Code
Dec 12, 2016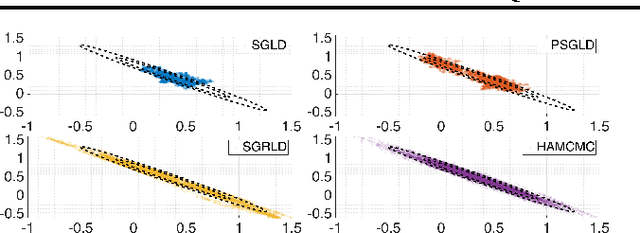
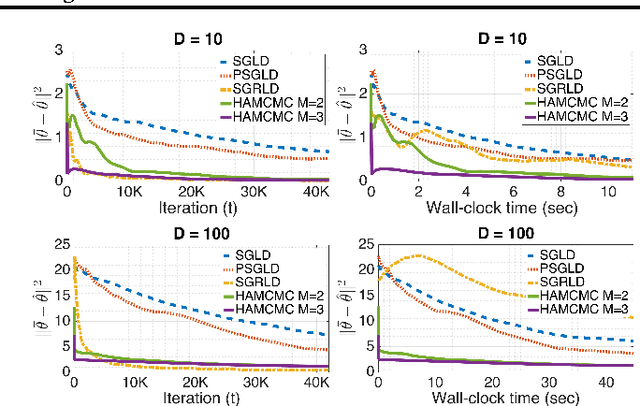
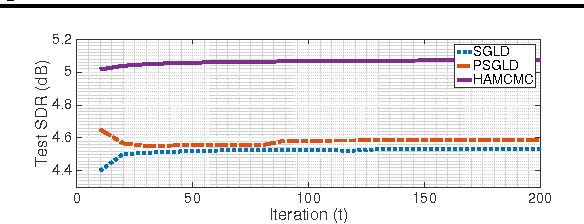
Recently, Stochastic Gradient Markov Chain Monte Carlo (SG-MCMC) methods have been proposed for scaling up Monte Carlo computations to large data problems. Whilst these approaches have proven useful in many applications, vanilla SG-MCMC might suffer from poor mixing rates when random variables exhibit strong couplings under the target densities or big scale differences. In this study, we propose a novel SG-MCMC method that takes the local geometry into account by using ideas from Quasi-Newton optimization methods. These second order methods directly approximate the inverse Hessian by using a limited history of samples and their gradients. Our method uses dense approximations of the inverse Hessian while keeping the time and memory complexities linear with the dimension of the problem. We provide a formal theoretical analysis where we show that the proposed method is asymptotically unbiased and consistent with the posterior expectations. We illustrate the effectiveness of the approach on both synthetic and real datasets. Our experiments on two challenging applications show that our method achieves fast convergence rates similar to Riemannian approaches while at the same time having low computational requirements similar to diagonal preconditioning approaches.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge