Unsupervised Audio Source Separation Using Differentiable Parametric Source Models

Supervised deep learning approaches to underdetermined audio source separation achieve state-of-the-art performance but require a dataset of mixtures along with their corresponding isolated source signals. Such datasets can be extremely costly to obtain for musical mixtures. This raises a need for unsupervised methods. We propose a novel unsupervised model-based deep learning approach to musical source separation. Each source is modelled with a differentiable parametric source-filter model. A neural network is trained to reconstruct the observed mixture as a sum of the sources by estimating the source models' parameters given their fundamental frequencies. At test time, soft masks are obtained from the synthesized source signals. The experimental evaluation on a vocal ensemble separation task shows that the proposed method outperforms learning-free methods based on nonnegative matrix factorization and a supervised deep learning baseline. Integrating domain knowledge in the form of source models into a data-driven method leads to high data efficiency: the proposed approach achieves good separation quality even when trained on less than three minutes of audio. This work makes powerful deep learning based separation usable in scenarios where training data with ground truth is expensive or nonexistent.

Fast Approximation of the Sliced-Wasserstein Distance Using Concentration of Random Projections

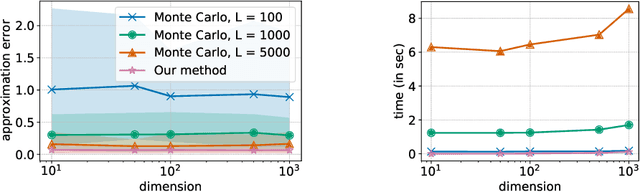
The Sliced-Wasserstein distance (SW) is being increasingly used in machine learning applications as an alternative to the Wasserstein distance and offers significant computational and statistical benefits. Since it is defined as an expectation over random projections, SW is commonly approximated by Monte Carlo. We adopt a new perspective to approximate SW by making use of the concentration of measure phenomenon: under mild assumptions, one-dimensional projections of a high-dimensional random vector are approximately Gaussian. Based on this observation, we develop a simple deterministic approximation for SW. Our method does not require sampling a number of random projections, and is therefore both accurate and easy to use compared to the usual Monte Carlo approximation. We derive nonasymptotical guarantees for our approach, and show that the approximation error goes to zero as the dimension increases, under a weak dependence condition on the data distribution. We validate our theoretical findings on synthetic datasets, and illustrate the proposed approximation on a generative modeling problem.

Approximate Bayesian Computation with the Sliced-Wasserstein Distance

Approximate Bayesian Computation (ABC) is a popular method for approximate inference in generative models with intractable but easy-to-sample likelihood. It constructs an approximate posterior distribution by finding parameters for which the simulated data are close to the observations in terms of summary statistics. These statistics are defined beforehand and might induce a loss of information, which has been shown to deteriorate the quality of the approximation. To overcome this problem, Wasserstein-ABC has been recently proposed, and compares the datasets via the Wasserstein distance between their empirical distributions, but does not scale well to the dimension or the number of samples. We propose a new ABC technique, called Sliced-Wasserstein ABC and based on the Sliced-Wasserstein distance, which has better computational and statistical properties. We derive two theoretical results showing the asymptotical consistency of our approach, and we illustrate its advantages on synthetic data and an image denoising task.

Asymptotic Guarantees for Learning Generative Models with the Sliced-Wasserstein Distance

Minimum expected distance estimation (MEDE) algorithms have been widely used for probabilistic models with intractable likelihood functions and they have become increasingly popular due to their use in implicit generative modeling (e.g. Wasserstein generative adversarial networks, Wasserstein autoencoders). Emerging from computational optimal transport, the Sliced-Wasserstein (SW) distance has become a popular choice in MEDE thanks to its simplicity and computational benefits. While several studies have reported empirical success on generative modeling with SW, the theoretical properties of such estimators have not yet been established. In this study, we investigate the asymptotic properties of estimators that are obtained by minimizing SW. We first show that convergence in SW implies weak convergence of probability measures in general Wasserstein spaces. Then we show that estimators obtained by minimizing SW (and also an approximate version of SW) are asymptotically consistent. We finally prove a central limit theorem, which characterizes the asymptotic distribution of the estimators and establish a convergence rate of $\sqrt{n}$, where $n$ denotes the number of observed data points. We illustrate the validity of our theory on both synthetic data and neural networks.

Generalized Sliced Wasserstein Distances

The Wasserstein distance and its variations, e.g., the sliced-Wasserstein (SW) distance, have recently drawn attention from the machine learning community. The SW distance, specifically, was shown to have similar properties to the Wasserstein distance, while being much simpler to compute, and is therefore used in various applications including generative modeling and general supervised/unsupervised learning. In this paper, we first clarify the mathematical connection between the SW distance and the Radon transform. We then utilize the generalized Radon transform to define a new family of distances for probability measures, which we call generalized sliced-Wasserstein (GSW) distances. We also show that, similar to the SW distance, the GSW distance can be extended to a maximum GSW (max-GSW) distance. We then provide the conditions under which GSW and max-GSW distances are indeed distances. Finally, we compare the numerical performance of the proposed distances on several generative modeling tasks, including SW flows and SW auto-encoders.

Stochastic Quasi-Newton Langevin Monte Carlo

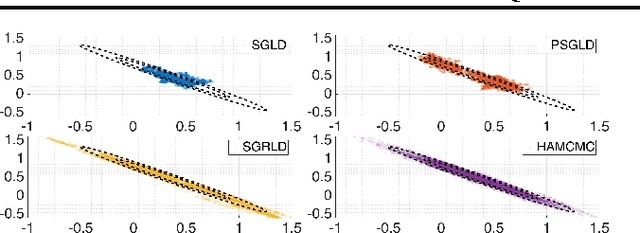
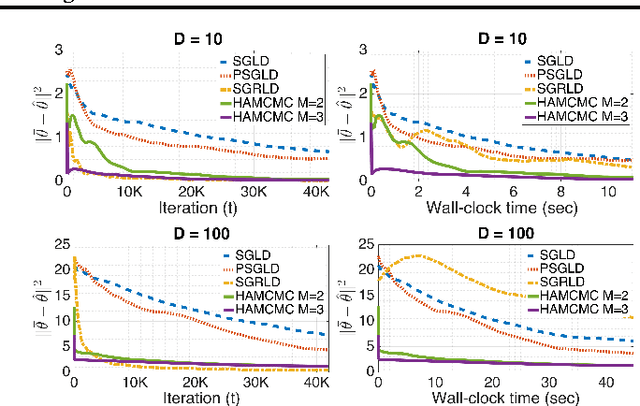
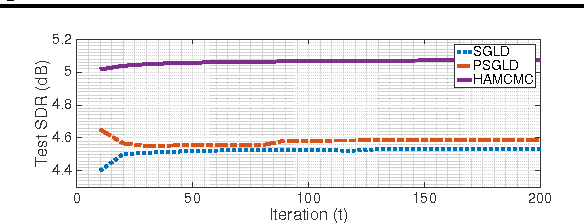
Recently, Stochastic Gradient Markov Chain Monte Carlo (SG-MCMC) methods have been proposed for scaling up Monte Carlo computations to large data problems. Whilst these approaches have proven useful in many applications, vanilla SG-MCMC might suffer from poor mixing rates when random variables exhibit strong couplings under the target densities or big scale differences. In this study, we propose a novel SG-MCMC method that takes the local geometry into account by using ideas from Quasi-Newton optimization methods. These second order methods directly approximate the inverse Hessian by using a limited history of samples and their gradients. Our method uses dense approximations of the inverse Hessian while keeping the time and memory complexities linear with the dimension of the problem. We provide a formal theoretical analysis where we show that the proposed method is asymptotically unbiased and consistent with the posterior expectations. We illustrate the effectiveness of the approach on both synthetic and real datasets. Our experiments on two challenging applications show that our method achieves fast convergence rates similar to Riemannian approaches while at the same time having low computational requirements similar to diagonal preconditioning approaches.