Y. Kenan Yilmaz
Generalized Beta Divergence
Jun 18, 2013



Abstract:This paper generalizes beta divergence beyond its classical form associated with power variance functions of Tweedie models. Generalized form is represented by a compact definite integral as a function of variance function of the exponential dispersion model. This compact integral form simplifies derivations of many properties such as scaling, translation and expectation of the beta divergence. Further, we show that beta divergence and (half of) the statistical deviance are equivalent measures.
Alpha/Beta Divergences and Tweedie Models
Sep 19, 2012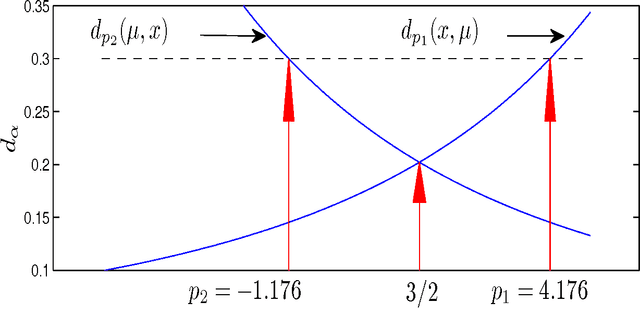
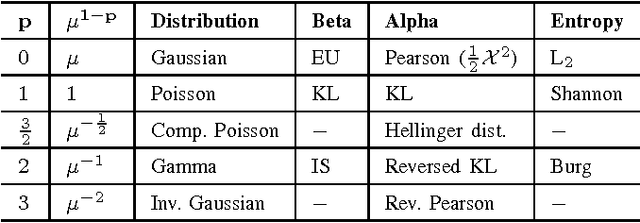
Abstract:We describe the underlying probabilistic interpretation of alpha and beta divergences. We first show that beta divergences are inherently tied to Tweedie distributions, a particular type of exponential family, known as exponential dispersion models. Starting from the variance function of a Tweedie model, we outline how to get alpha and beta divergences as special cases of Csisz\'ar's $f$ and Bregman divergences. This result directly generalizes the well-known relationship between the Gaussian distribution and least squares estimation to Tweedie models and beta divergence minimization.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge