POEMS: Product of Experts for Interpretable Multi-omic Integration using Sparse Decoding

Integrating different molecular layers, i.e., multiomics data, is crucial for unraveling the complexity of diseases; yet, most deep generative models either prioritize predictive performance at the expense of interpretability or enforce interpretability by linearizing the decoder, thereby weakening the network's nonlinear expressiveness. To overcome this tradeoff, we introduce POEMS: Product Of Experts for Interpretable Multiomics Integration using Sparse Decoding, an unsupervised probabilistic framework that preserves predictive performance while providing interpretability. POEMS provides interpretability without linearizing any part of the network by 1) mapping features to latent factors using sparse connections, which directly translates to biomarker discovery, 2) allowing for cross-omic associations through a shared latent space using product of experts model, and 3) reporting contributions of each omic by a gating network that adaptively computes their influence in the representation learning. Additionally, we present an efficient sparse decoder. In a cancer subtyping case study, POEMS achieves competitive clustering and classification performance while offering our novel set of interpretations, demonstrating that biomarker based insight and predictive accuracy can coexist in multiomics representation learning.

VaiPhy: a Variational Inference Based Algorithm for Phylogeny

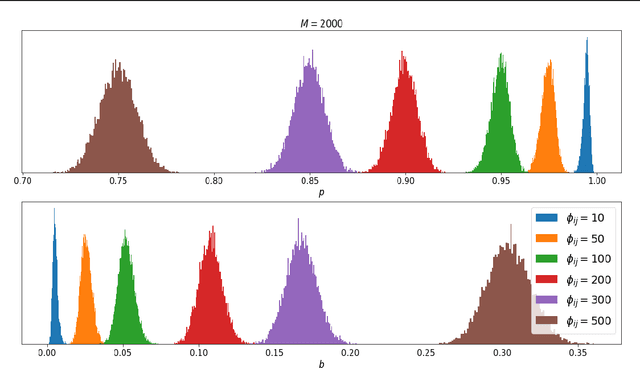
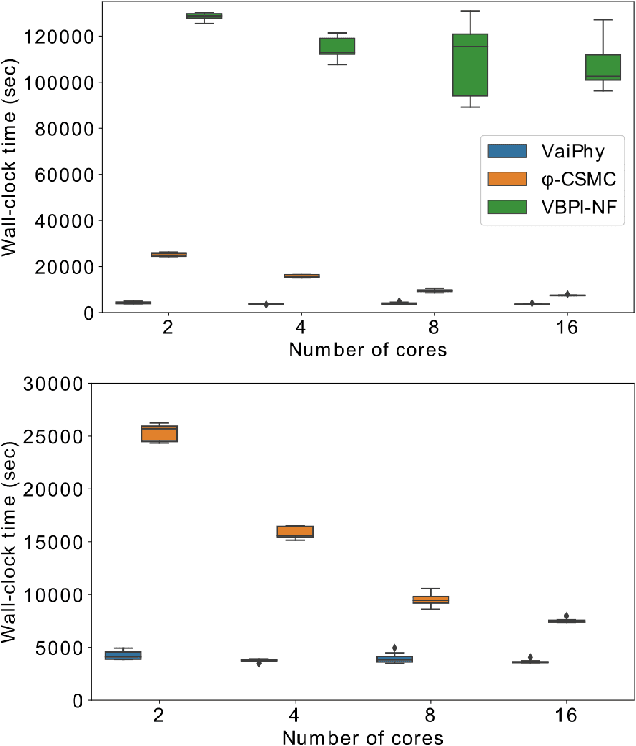
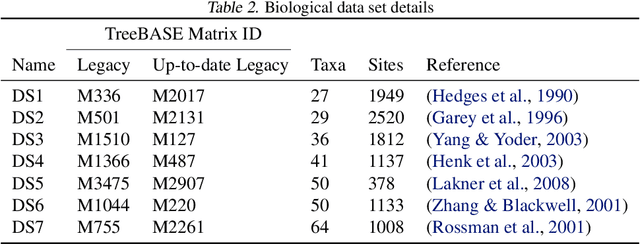
Phylogenetics is a classical methodology in computational biology that today has become highly relevant for medical investigation of single-cell data, e.g., in the context of development of cancer. The exponential size of the tree space is unfortunately a formidable obstacle for current Bayesian phylogenetic inference using Markov chain Monte Carlo based methods since these rely on local operations. And although more recent variational inference (VI) based methods offer speed improvements, they rely on expensive auto-differentiation operations for learning the variational parameters. We propose VaiPhy, a remarkably fast VI based algorithm for approximate posterior inference in an augmented tree space. VaiPhy produces marginal log-likelihood estimates on par with the state-of-the-art methods on real data, and is considerably faster since it does not require auto-differentiation. Instead, VaiPhy combines coordinate ascent update equations with two novel sampling schemes: (i) SLANTIS, a proposal distribution for tree topologies in the augmented tree space, and (ii) the JC sampler, the, to the best of our knowledge, first ever scheme for sampling branch lengths directly from the popular Jukes-Cantor model. We compare VaiPhy in terms of density estimation and runtime. Additionally, we evaluate the reproducibility of the baselines. We provide our code on GitHub: https://github.com/Lagergren-Lab/VaiPhy.

Towards interpretability of Mixtures of Hidden Markov Models

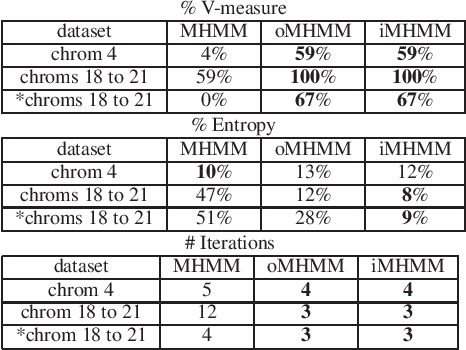
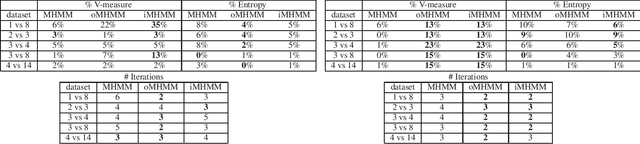
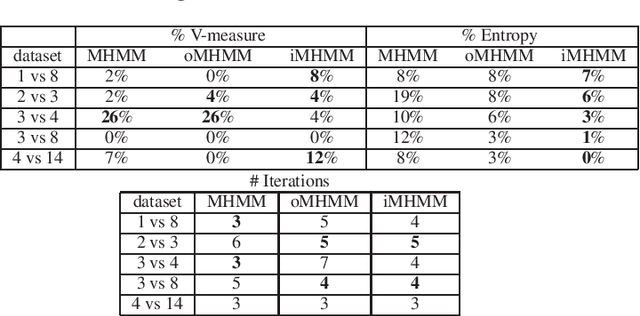
Mixtures of Hidden Markov Models (MHMMs) are frequently used for clustering of sequential data. An important aspect of MHMMs, as of any clustering approach, is that they can be interpretable, allowing for novel insights to be gained from the data. However, without a proper way of measuring interpretability, the evaluation of novel contributions is difficult and it becomes practically impossible to devise techniques that directly optimize this property. In this work, an information-theoretic measure (entropy) is proposed for interpretability of MHMMs, and based on that, a novel approach to improve model interpretability is proposed, i.e., an entropy-regularized Expectation Maximization (EM) algorithm. The new approach aims for reducing the entropy of the Markov chains (involving state transition matrices) within an MHMM, i.e., assigning higher weights to common state transitions during clustering. It is argued that this entropy reduction, in general, leads to improved interpretability since the most influential and important state transitions of the clusters can be more easily identified. An empirical investigation shows that it is possible to improve the interpretability of MHMMs, as measured by entropy, without sacrificing (but rather improving) clustering performance and computational costs, as measured by the v-measure and number of EM iterations, respectively.