Towards interpretability of Mixtures of Hidden Markov Models

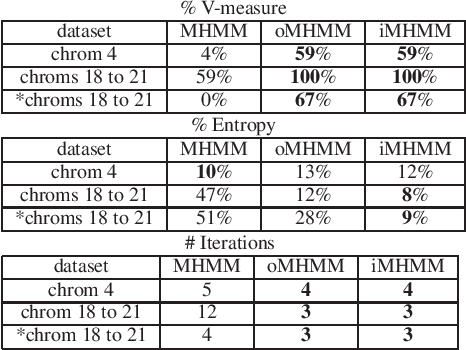
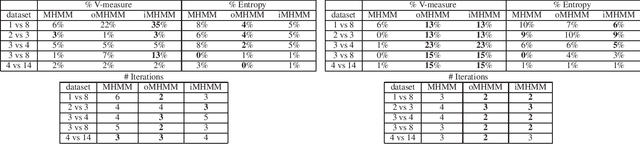
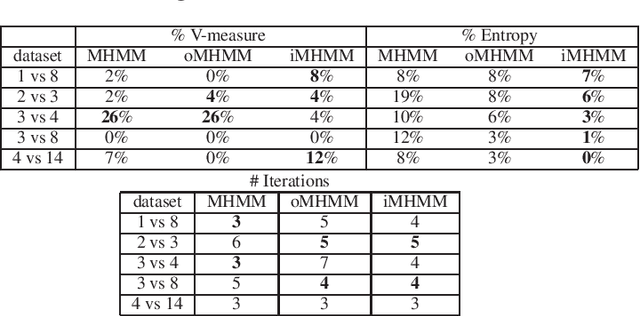
Mixtures of Hidden Markov Models (MHMMs) are frequently used for clustering of sequential data. An important aspect of MHMMs, as of any clustering approach, is that they can be interpretable, allowing for novel insights to be gained from the data. However, without a proper way of measuring interpretability, the evaluation of novel contributions is difficult and it becomes practically impossible to devise techniques that directly optimize this property. In this work, an information-theoretic measure (entropy) is proposed for interpretability of MHMMs, and based on that, a novel approach to improve model interpretability is proposed, i.e., an entropy-regularized Expectation Maximization (EM) algorithm. The new approach aims for reducing the entropy of the Markov chains (involving state transition matrices) within an MHMM, i.e., assigning higher weights to common state transitions during clustering. It is argued that this entropy reduction, in general, leads to improved interpretability since the most influential and important state transitions of the clusters can be more easily identified. An empirical investigation shows that it is possible to improve the interpretability of MHMMs, as measured by entropy, without sacrificing (but rather improving) clustering performance and computational costs, as measured by the v-measure and number of EM iterations, respectively.