Medical Image Segmentation with SAM-generated Annotations

The field of medical image segmentation is hindered by the scarcity of large, publicly available annotated datasets. Not all datasets are made public for privacy reasons, and creating annotations for a large dataset is time-consuming and expensive, as it requires specialized expertise to accurately identify regions of interest (ROIs) within the images. To address these challenges, we evaluate the performance of the Segment Anything Model (SAM) as an annotation tool for medical data by using it to produce so-called "pseudo labels" on the Medical Segmentation Decathlon (MSD) computed tomography (CT) tasks. The pseudo labels are then used in place of ground truth labels to train a UNet model in a weakly-supervised manner. We experiment with different prompt types on SAM and find that the bounding box prompt is a simple yet effective method for generating pseudo labels. This method allows us to develop a weakly-supervised model that performs comparably to a fully supervised model.

Indirectly Parameterized Concrete Autoencoders

Feature selection is a crucial task in settings where data is high-dimensional or acquiring the full set of features is costly. Recent developments in neural network-based embedded feature selection show promising results across a wide range of applications. Concrete Autoencoders (CAEs), considered state-of-the-art in embedded feature selection, may struggle to achieve stable joint optimization, hurting their training time and generalization. In this work, we identify that this instability is correlated with the CAE learning duplicate selections. To remedy this, we propose a simple and effective improvement: Indirectly Parameterized CAEs (IP-CAEs). IP-CAEs learn an embedding and a mapping from it to the Gumbel-Softmax distributions' parameters. Despite being simple to implement, IP-CAE exhibits significant and consistent improvements over CAE in both generalization and training time across several datasets for reconstruction and classification. Unlike CAE, IP-CAE effectively leverages non-linear relationships and does not require retraining the jointly optimized decoder. Furthermore, our approach is, in principle, generalizable to Gumbel-Softmax distributions beyond feature selection.

Logistic-Normal Likelihoods for Heteroscedastic Label Noise in Classification

A natural way of estimating heteroscedastic label noise in regression is to model the observed (potentially noisy) target as a sample from a normal distribution, whose parameters can be learned by minimizing the negative log-likelihood. This loss has desirable loss attenuation properties, as it can reduce the contribution of high-error examples. Intuitively, this behavior can improve robustness against label noise by reducing overfitting. We propose an extension of this simple and probabilistic approach to classification that has the same desirable loss attenuation properties. We evaluate the effectiveness of the method by measuring its robustness against label noise in classification. We perform enlightening experiments exploring the inner workings of the method, including sensitivity to hyperparameters, ablation studies, and more.

Deep Double Descent via Smooth Interpolation

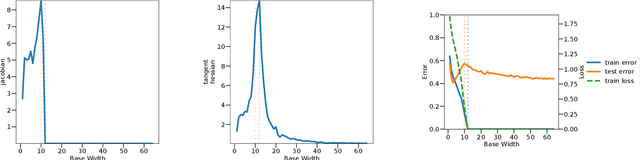
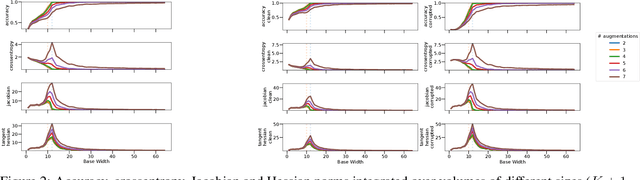
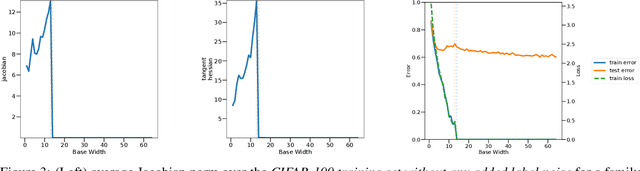
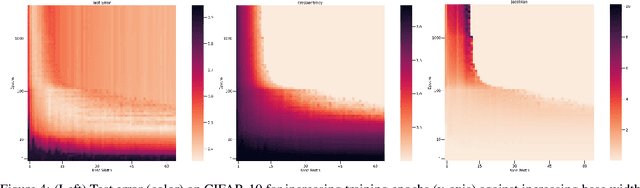
Overparameterized deep networks are known to be able to perfectly fit the training data while at the same time showing good generalization performance. A common paradigm drawn from intuition on linear regression suggests that large networks are able to interpolate even noisy data, without considerably deviating from the ground-truth signal. At present, a precise characterization of this phenomenon is missing. In this work, we present an empirical study of sharpness of the loss landscape of deep networks as we systematically control the number of model parameters and training epochs. We extend our study to neighbourhoods of the training data, as well as around cleanly- and noisily-labelled samples. Our findings show that the loss sharpness in the input space follows both model- and epoch-wise double descent, with worse peaks observed around noisy labels. While small interpolating models sharply fit both clean and noisy data, large models express a smooth and flat loss landscape, in contrast with existing intuition.

Consistency Regularization Can Improve Robustness to Label Noise

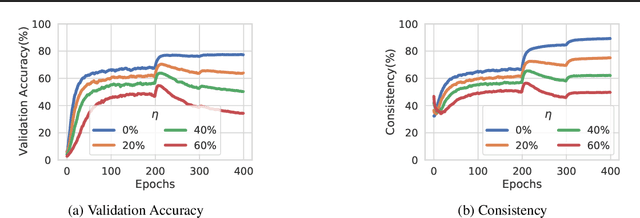
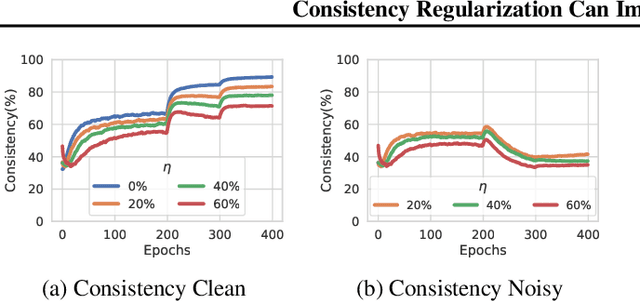
Consistency regularization is a commonly-used technique for semi-supervised and self-supervised learning. It is an auxiliary objective function that encourages the prediction of the network to be similar in the vicinity of the observed training samples. Hendrycks et al. (2020) have recently shown such regularization naturally brings test-time robustness to corrupted data and helps with calibration. This paper empirically studies the relevance of consistency regularization for training-time robustness to noisy labels. First, we make two interesting and useful observations regarding the consistency of networks trained with the standard cross entropy loss on noisy datasets which are: (i) networks trained on noisy data have lower consistency than those trained on clean data, and(ii) the consistency reduces more significantly around noisy-labelled training data points than correctly-labelled ones. Then, we show that a simple loss function that encourages consistency improves the robustness of the models to label noise on both synthetic (CIFAR-10, CIFAR-100) and real-world (WebVision) noise as well as different noise rates and types and achieves state-of-the-art results.

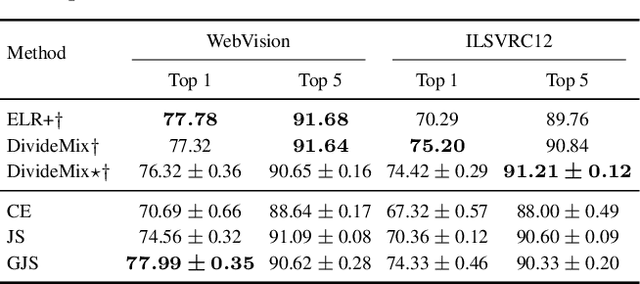
Generalized Jensen-Shannon Divergence Loss for Learning with Noisy Labels

Prior works have found it beneficial to combine provably noise-robust loss functions e.g., mean absolute error (MAE) with standard categorical loss function e.g. cross entropy (CE) to improve their learnability. Here, we propose to use Jensen-Shannon divergence as a noise-robust loss function and show that it interestingly interpolate between CE and MAE with a controllable mixing parameter. Furthermore, we make a crucial observation that CE exhibit lower consistency around noisy data points. Based on this observation, we adopt a generalized version of the Jensen-Shannon divergence for multiple distributions to encourage consistency around data points. Using this loss function, we show state-of-the-art results on both synthetic (CIFAR), and real-world (WebVision) noise with varying noise rates.

Efficient Evaluation-Time Uncertainty Estimation by Improved Distillation

In this work we aim to obtain computationally-efficient uncertainty estimates with deep networks. For this, we propose a modified knowledge distillation procedure that achieves state-of-the-art uncertainty estimates both for in and out-of-distribution samples. Our contributions include a) demonstrating and adapting to distillation's regularization effect b) proposing a novel target teacher distribution c) a simple augmentation procedure to improve out-of-distribution uncertainty estimates d) shedding light on the distillation procedure through comprehensive set of experiments.