On the Lipschitz Constant of Deep Networks and Double Descent

Existing bounds on the generalization error of deep networks assume some form of smooth or bounded dependence on the input variable, falling short of investigating the mechanisms controlling such factors in practice. In this work, we present an extensive experimental study of the empirical Lipschitz constant of deep networks undergoing double descent, and highlight non-monotonic trends strongly correlating with the test error. Building a connection between parameter-space and input-space gradients for SGD around a critical point, we isolate two important factors -- namely loss landscape curvature and distance of parameters from initialization -- respectively controlling optimization dynamics around a critical point and bounding model function complexity, even beyond the training data. Our study presents novels insights on implicit regularization via overparameterization, and effective model complexity for networks trained in practice.

Deep Double Descent via Smooth Interpolation

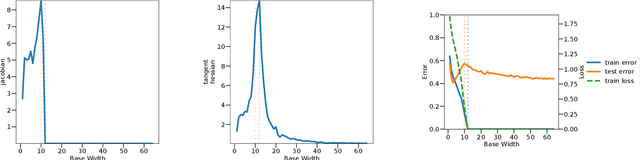
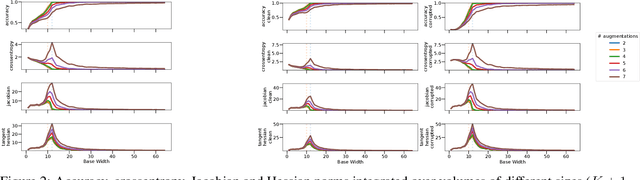
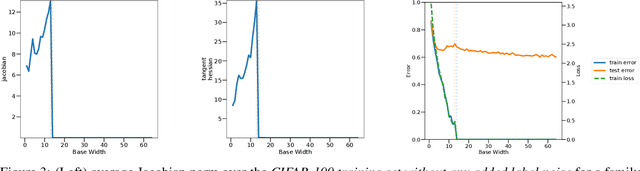
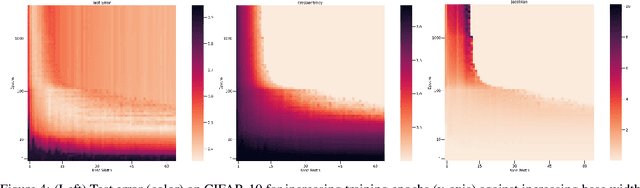
Overparameterized deep networks are known to be able to perfectly fit the training data while at the same time showing good generalization performance. A common paradigm drawn from intuition on linear regression suggests that large networks are able to interpolate even noisy data, without considerably deviating from the ground-truth signal. At present, a precise characterization of this phenomenon is missing. In this work, we present an empirical study of sharpness of the loss landscape of deep networks as we systematically control the number of model parameters and training epochs. We extend our study to neighbourhoods of the training data, as well as around cleanly- and noisily-labelled samples. Our findings show that the loss sharpness in the input space follows both model- and epoch-wise double descent, with worse peaks observed around noisy labels. While small interpolating models sharply fit both clean and noisy data, large models express a smooth and flat loss landscape, in contrast with existing intuition.

Are All Linear Regions Created Equal?

The number of linear regions has been studied as a proxy of complexity for ReLU networks. However, the empirical success of network compression techniques like pruning and knowledge distillation, suggest that in the overparameterized setting, linear regions density might fail to capture the effective nonlinearity. In this work, we propose an efficient algorithm for discovering linear regions and use it to investigate the effectiveness of density in capturing the nonlinearity of trained VGGs and ResNets on CIFAR-10 and CIFAR-100. We contrast the results with a more principled nonlinearity measure based on function variation, highlighting the shortcomings of linear regions density. Furthermore, interestingly, our measure of nonlinearity clearly correlates with model-wise deep double descent, connecting reduced test error with reduced nonlinearity, and increased local similarity of linear regions.

Hyperplane Arrangements of Trained ConvNets Are Biased

We investigate the geometric properties of the functions learned by trained ConvNets in the preactivation space of their convolutional layers, by performing an empirical study of hyperplane arrangements induced by a convolutional layer. We introduce statistics over the weights of a trained network to study local arrangements and relate them to the training dynamics. We observe that trained ConvNets show a significant statistical bias towards regular hyperplane configurations. Furthermore, we find that layers showing biased configurations are critical to validation performance for the architectures considered, trained on CIFAR10, CIFAR100 and ImageNet.