Deep Double Descent via Smooth Interpolation

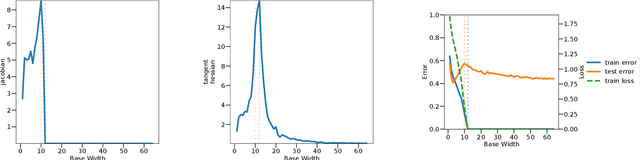
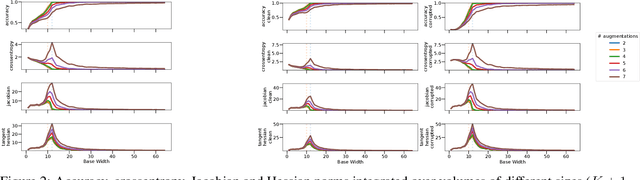
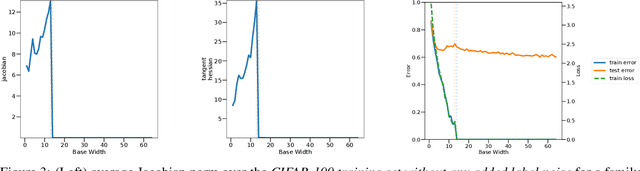
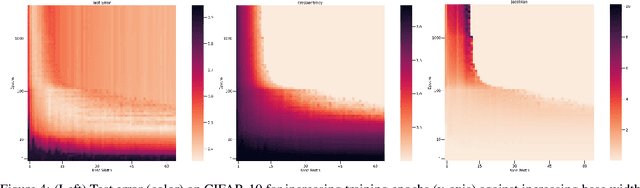
Overparameterized deep networks are known to be able to perfectly fit the training data while at the same time showing good generalization performance. A common paradigm drawn from intuition on linear regression suggests that large networks are able to interpolate even noisy data, without considerably deviating from the ground-truth signal. At present, a precise characterization of this phenomenon is missing. In this work, we present an empirical study of sharpness of the loss landscape of deep networks as we systematically control the number of model parameters and training epochs. We extend our study to neighbourhoods of the training data, as well as around cleanly- and noisily-labelled samples. Our findings show that the loss sharpness in the input space follows both model- and epoch-wise double descent, with worse peaks observed around noisy labels. While small interpolating models sharply fit both clean and noisy data, large models express a smooth and flat loss landscape, in contrast with existing intuition.