Gerrit Großmann
The Power of Stories: Narrative Priming Shapes How LLM Agents Collaborate and Compete
May 08, 2025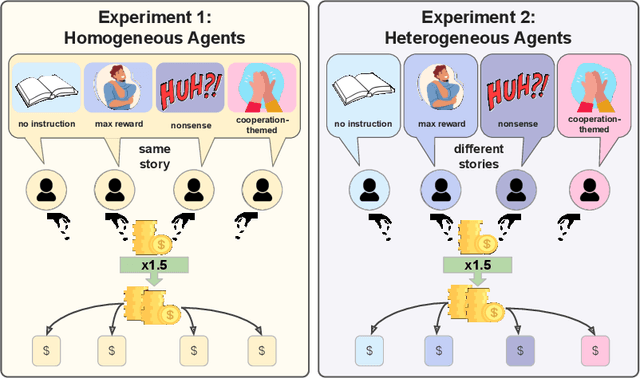
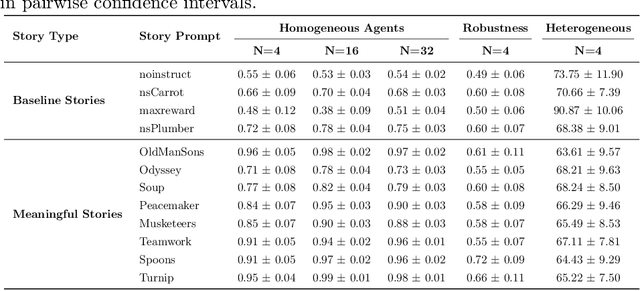
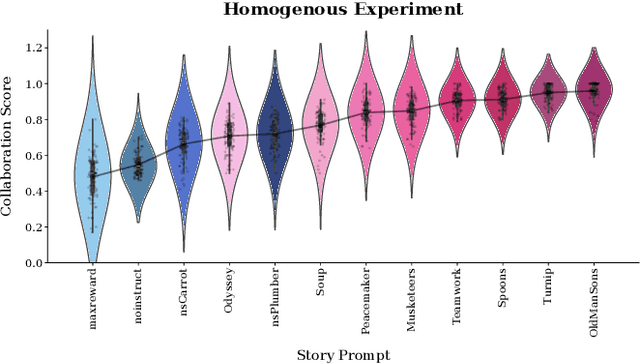
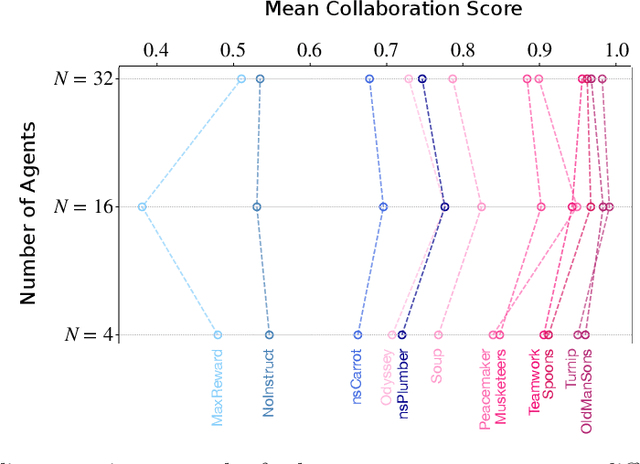
Abstract:According to Yuval Noah Harari, large-scale human cooperation is driven by shared narratives that encode common beliefs and values. This study explores whether such narratives can similarly nudge LLM agents toward collaboration. We use a finitely repeated public goods game in which LLM agents choose either cooperative or egoistic spending strategies. We prime agents with stories highlighting teamwork to different degrees and test how this influences negotiation outcomes. Our experiments explore four questions:(1) How do narratives influence negotiation behavior? (2) What differs when agents share the same story versus different ones? (3) What happens when the agent numbers grow? (4) Are agents resilient against self-serving negotiators? We find that story-based priming significantly affects negotiation strategies and success rates. Common stories improve collaboration, benefiting each agent. By contrast, priming agents with different stories reverses this effect, and those agents primed toward self-interest prevail. We hypothesize that these results carry implications for multi-agent system design and AI alignment.
When Counterfactual Reasoning Fails: Chaos and Real-World Complexity
Apr 01, 2025Abstract:Counterfactual reasoning, a cornerstone of human cognition and decision-making, is often seen as the 'holy grail' of causal learning, with applications ranging from interpreting machine learning models to promoting algorithmic fairness. While counterfactual reasoning has been extensively studied in contexts where the underlying causal model is well-defined, real-world causal modeling is often hindered by model and parameter uncertainty, observational noise, and chaotic behavior. The reliability of counterfactual analysis in such settings remains largely unexplored. In this work, we investigate the limitations of counterfactual reasoning within the framework of Structural Causal Models. Specifically, we empirically investigate \emph{counterfactual sequence estimation} and highlight cases where it becomes increasingly unreliable. We find that realistic assumptions, such as low degrees of model uncertainty or chaotic dynamics, can result in counterintuitive outcomes, including dramatic deviations between predicted and true counterfactual trajectories. This work urges caution when applying counterfactual reasoning in settings characterized by chaos and uncertainty. Furthermore, it raises the question of whether certain systems may pose fundamental limitations on the ability to answer counterfactual questions about their behavior.
CleanSurvival: Automated data preprocessing for time-to-event models using reinforcement learning
Feb 06, 2025



Abstract:Data preprocessing is a critical yet frequently neglected aspect of machine learning, often paid little attention despite its potentially significant impact on model performance. While automated machine learning pipelines are starting to recognize and integrate data preprocessing into their solutions for classification and regression tasks, this integration is lacking for more specialized tasks like survival or time-to-event models. As a result, survival analysis not only faces the general challenges of data preprocessing but also suffers from the lack of tailored, automated solutions in this area. To address this gap, this paper presents 'CleanSurvival', a reinforcement-learning-based solution for optimizing preprocessing pipelines, extended specifically for survival analysis. The framework can handle continuous and categorical variables, using Q-learning to select which combination of data imputation, outlier detection and feature extraction techniques achieves optimal performance for a Cox, random forest, neural network or user-supplied time-to-event model. The package is available on GitHub: https://github.com/datasciapps/CleanSurvival Experimental benchmarks on real-world datasets show that the Q-learning-based data preprocessing results in superior predictive performance to standard approaches, finding such a model up to 10 times faster than undirected random grid search. Furthermore, a simulation study demonstrates the effectiveness in different types and levels of missingness and noise in the data.
Enhancing GNNs with Architecture-Agnostic Graph Transformations: A Systematic Analysis
Oct 11, 2024Abstract:In recent years, a wide variety of graph neural network (GNN) architectures have emerged, each with its own strengths, weaknesses, and complexities. Various techniques, including rewiring, lifting, and node annotation with centrality values, have been employed as pre-processing steps to enhance GNN performance. However, there are no universally accepted best practices, and the impact of architecture and pre-processing on performance often remains opaque. This study systematically explores the impact of various graph transformations as pre-processing steps on the performance of common GNN architectures across standard datasets. The models are evaluated based on their ability to distinguish non-isomorphic graphs, referred to as expressivity. Our findings reveal that certain transformations, particularly those augmenting node features with centrality measures, consistently improve expressivity. However, these gains come with trade-offs, as methods like graph encoding, while enhancing expressivity, introduce numerical inaccuracies widely-used python packages. Additionally, we observe that these pre-processing techniques are limited when addressing complex tasks involving 3-WL and 4-WL indistinguishable graphs.
GINA: Neural Relational Inference From Independent Snapshots
May 29, 2021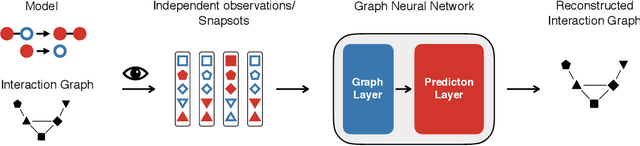
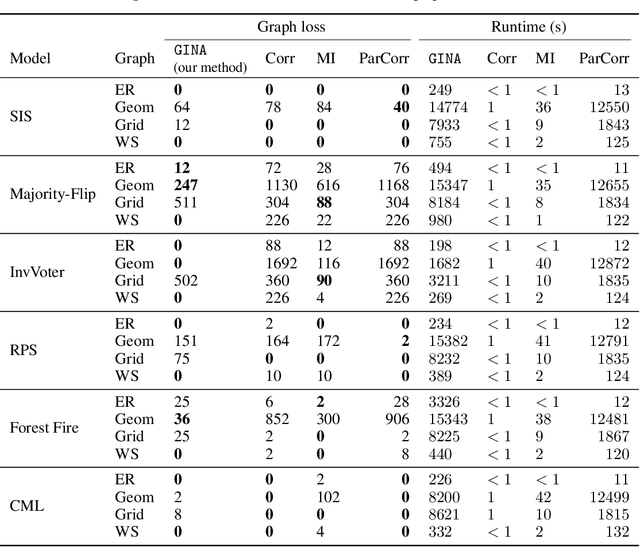
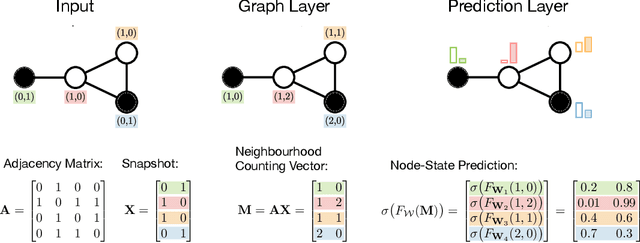
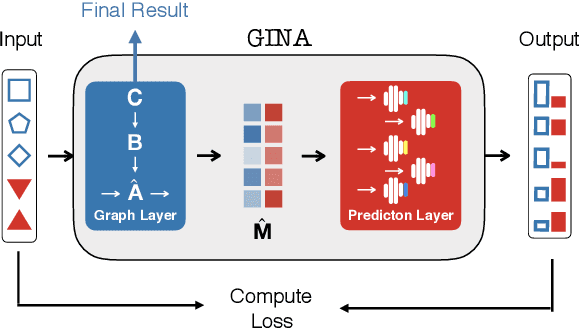
Abstract:Dynamical systems in which local interactions among agents give rise to complex emerging phenomena are ubiquitous in nature and society. This work explores the problem of inferring the unknown interaction structure (represented as a graph) of such a system from measurements of its constituent agents or individual components (represented as nodes). We consider a setting where the underlying dynamical model is unknown and where different measurements (i.e., snapshots) may be independent (e.g., may stem from different experiments). We propose GINA (Graph Inference Network Architecture), a graph neural network (GNN) to simultaneously learn the latent interaction graph and, conditioned on the interaction graph, the prediction of a node's observable state based on adjacent vertices. GINA is based on the hypothesis that the ground truth interaction graph -- among all other potential graphs -- allows to predict the state of a node, given the states of its neighbors, with the highest accuracy. We test this hypothesis and demonstrate GINA's effectiveness on a wide range of interaction graphs and dynamical processes.
Abstraction-Guided Truncations for Stationary Distributions of Markov Population Models
May 03, 2021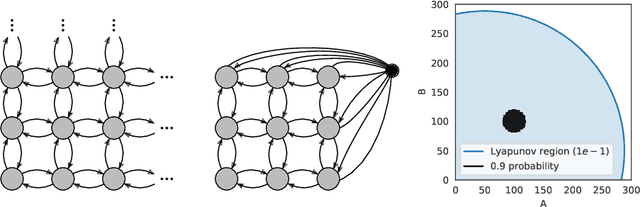
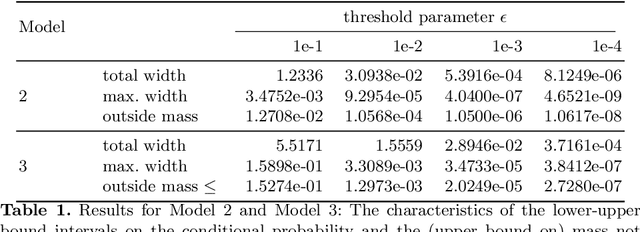
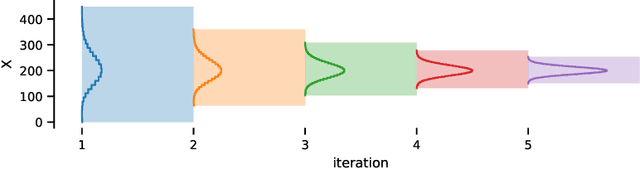
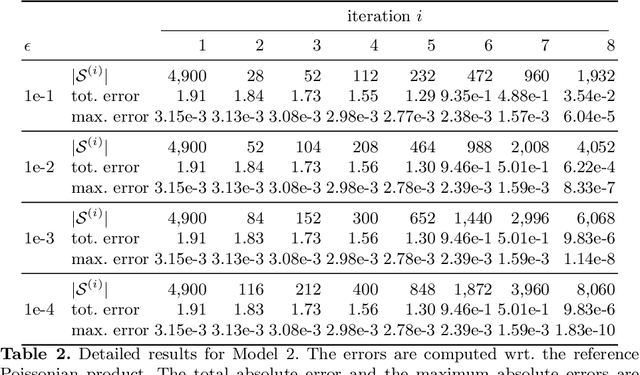
Abstract:To understand the long-run behavior of Markov population models, the computation of the stationary distribution is often a crucial part. We propose a truncation-based approximation that employs a state-space lumping scheme, aggregating states in a grid structure. The resulting approximate stationary distribution is used to iteratively refine relevant and truncate irrelevant parts of the state-space. This way, the algorithm learns a well-justified finite-state projection tailored to the stationary behavior. We demonstrate the method's applicability to a wide range of non-linear problems with complex stationary behaviors.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge