Michael Backenköhler
GINA: Neural Relational Inference From Independent Snapshots
May 29, 2021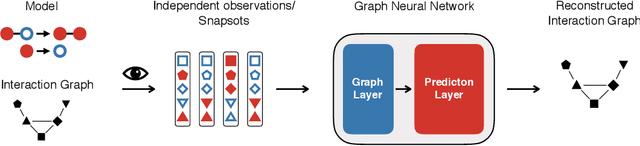
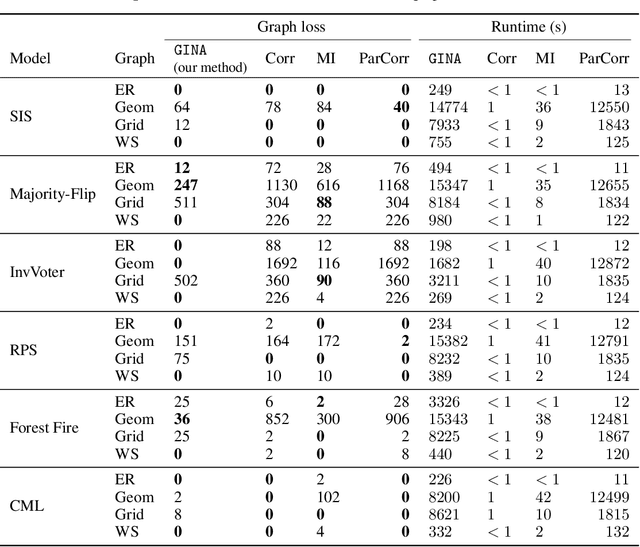
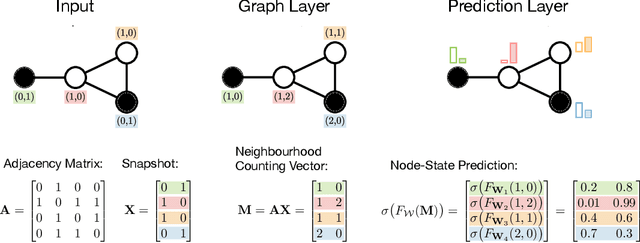
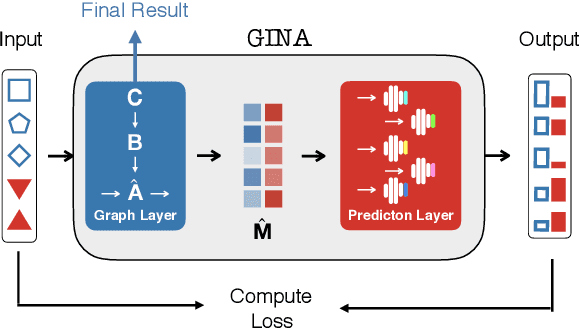
Abstract:Dynamical systems in which local interactions among agents give rise to complex emerging phenomena are ubiquitous in nature and society. This work explores the problem of inferring the unknown interaction structure (represented as a graph) of such a system from measurements of its constituent agents or individual components (represented as nodes). We consider a setting where the underlying dynamical model is unknown and where different measurements (i.e., snapshots) may be independent (e.g., may stem from different experiments). We propose GINA (Graph Inference Network Architecture), a graph neural network (GNN) to simultaneously learn the latent interaction graph and, conditioned on the interaction graph, the prediction of a node's observable state based on adjacent vertices. GINA is based on the hypothesis that the ground truth interaction graph -- among all other potential graphs -- allows to predict the state of a node, given the states of its neighbors, with the highest accuracy. We test this hypothesis and demonstrate GINA's effectiveness on a wide range of interaction graphs and dynamical processes.
Abstraction-Guided Truncations for Stationary Distributions of Markov Population Models
May 03, 2021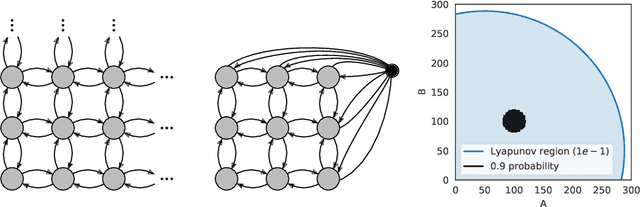
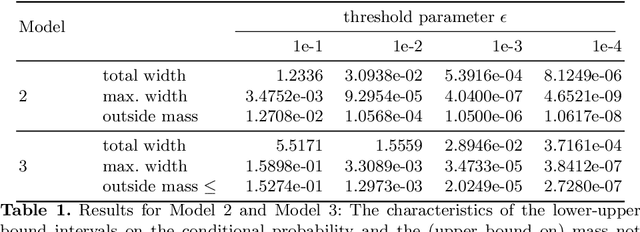
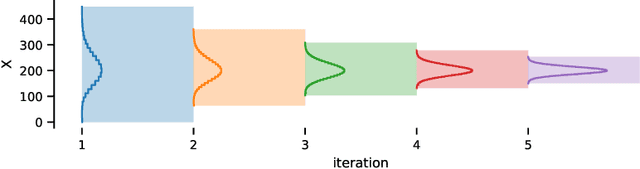
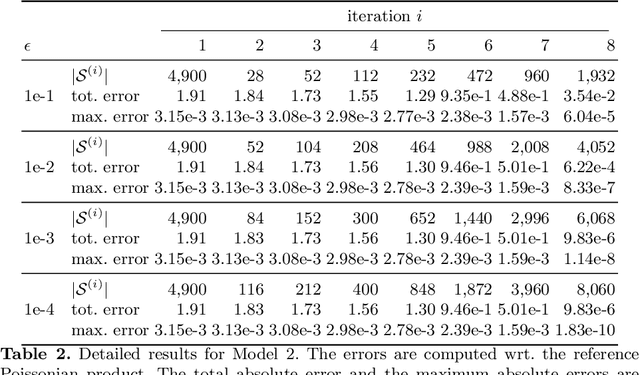
Abstract:To understand the long-run behavior of Markov population models, the computation of the stationary distribution is often a crucial part. We propose a truncation-based approximation that employs a state-space lumping scheme, aggregating states in a grid structure. The resulting approximate stationary distribution is used to iteratively refine relevant and truncate irrelevant parts of the state-space. This way, the algorithm learns a well-justified finite-state projection tailored to the stationary behavior. We demonstrate the method's applicability to a wide range of non-linear problems with complex stationary behaviors.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge