Abstraction-Guided Truncations for Stationary Distributions of Markov Population Models
Paper and Code
May 03, 2021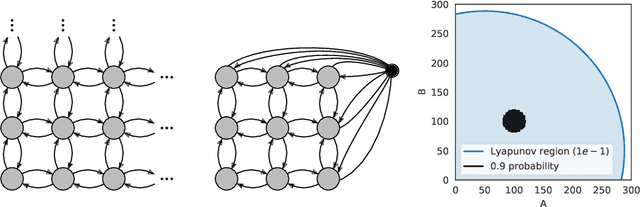
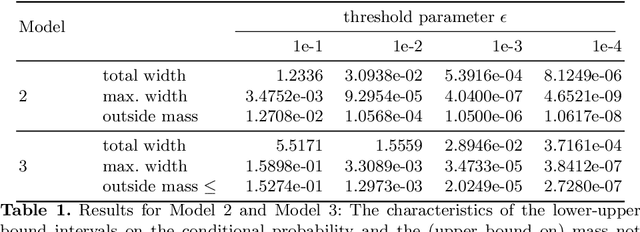
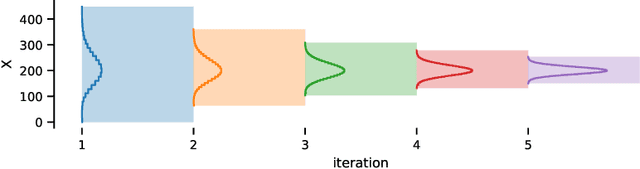
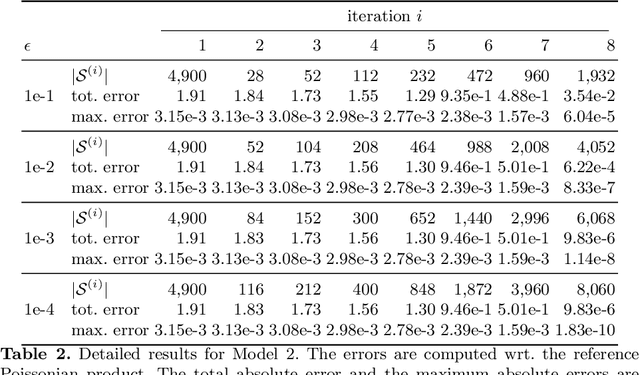
To understand the long-run behavior of Markov population models, the computation of the stationary distribution is often a crucial part. We propose a truncation-based approximation that employs a state-space lumping scheme, aggregating states in a grid structure. The resulting approximate stationary distribution is used to iteratively refine relevant and truncate irrelevant parts of the state-space. This way, the algorithm learns a well-justified finite-state projection tailored to the stationary behavior. We demonstrate the method's applicability to a wide range of non-linear problems with complex stationary behaviors.
* arXiv admin note: text overlap with arXiv:2010.10096
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge