NeuroAI for AI Safety

As AI systems become increasingly powerful, the need for safe AI has become more pressing. Humans are an attractive model for AI safety: as the only known agents capable of general intelligence, they perform robustly even under conditions that deviate significantly from prior experiences, explore the world safely, understand pragmatics, and can cooperate to meet their intrinsic goals. Intelligence, when coupled with cooperation and safety mechanisms, can drive sustained progress and well-being. These properties are a function of the architecture of the brain and the learning algorithms it implements. Neuroscience may thus hold important keys to technical AI safety that are currently underexplored and underutilized. In this roadmap, we highlight and critically evaluate several paths toward AI safety inspired by neuroscience: emulating the brain's representations, information processing, and architecture; building robust sensory and motor systems from imitating brain data and bodies; fine-tuning AI systems on brain data; advancing interpretability using neuroscience methods; and scaling up cognitively-inspired architectures. We make several concrete recommendations for how neuroscience can positively impact AI safety.

Combining Induction and Transduction for Abstract Reasoning

When learning an input-output mapping from very few examples, is it better to first infer a latent function that explains the examples, or is it better to directly predict new test outputs, e.g. using a neural network? We study this question on ARC, a highly diverse dataset of abstract reasoning tasks. We train neural models for induction (inferring latent functions) and transduction (directly predicting the test output for a given test input). Our models are trained on synthetic data generated by prompting LLMs to produce Python code specifying a function to be inferred, plus a stochastic subroutine for generating inputs to that function. We find inductive and transductive models solve very different problems, despite training on the same problems, and despite sharing the same neural architecture.

How does the primate brain combine generative and discriminative computations in vision?

Vision is widely understood as an inference problem. However, two contrasting conceptions of the inference process have each been influential in research on biological vision as well as the engineering of machine vision. The first emphasizes bottom-up signal flow, describing vision as a largely feedforward, discriminative inference process that filters and transforms the visual information to remove irrelevant variation and represent behaviorally relevant information in a format suitable for downstream functions of cognition and behavioral control. In this conception, vision is driven by the sensory data, and perception is direct because the processing proceeds from the data to the latent variables of interest. The notion of "inference" in this conception is that of the engineering literature on neural networks, where feedforward convolutional neural networks processing images are said to perform inference. The alternative conception is that of vision as an inference process in Helmholtz's sense, where the sensory evidence is evaluated in the context of a generative model of the causal processes giving rise to it. In this conception, vision inverts a generative model through an interrogation of the evidence in a process often thought to involve top-down predictions of sensory data to evaluate the likelihood of alternative hypotheses. The authors include scientists rooted in roughly equal numbers in each of the conceptions and motivated to overcome what might be a false dichotomy between them and engage the other perspective in the realm of theory and experiment. The primate brain employs an unknown algorithm that may combine the advantages of both conceptions. We explain and clarify the terminology, review the key empirical evidence, and propose an empirical research program that transcends the dichotomy and sets the stage for revealing the mysterious hybrid algorithm of primate vision.

The Random Conditional Distribution for Higher-Order Probabilistic Inference

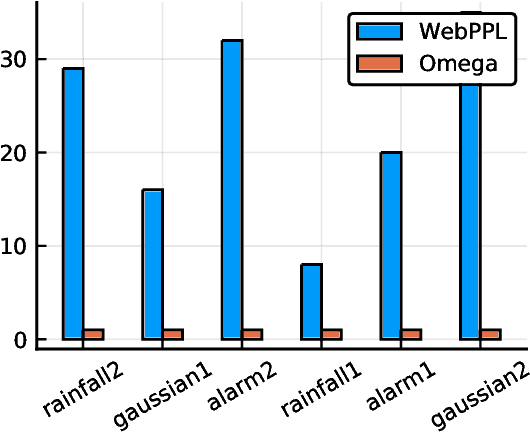
The need to condition distributional properties such as expectation, variance, and entropy arises in algorithmic fairness, model simplification, robustness and many other areas. At face value however, distributional properties are not random variables, and hence conditioning them is a semantic error and type error in probabilistic programming languages. On the other hand, distributional properties are contingent on other variables in the model, change in value when we observe more information, and hence in a precise sense are random variables too. In order to capture the uncertain over distributional properties, we introduce a probability construct -- the random conditional distribution -- and incorporate it into a probabilistic programming language Omega. A random conditional distribution is a higher-order random variable whose realizations are themselves conditional random variables. In Omega we extend distributional properties of random variables to random conditional distributions, such that for example while the expectation a real valued random variable is a real value, the expectation of a random conditional distribution is a distribution over expectations. As a consequence, it requires minimal syntax to encode inference problems over distributional properties, which so far have evaded treatment within probabilistic programming systems and probabilistic modeling in general. We demonstrate our approach case studies in algorithmic fairness and robustness.

Soft Constraints for Inference with Declarative Knowledge

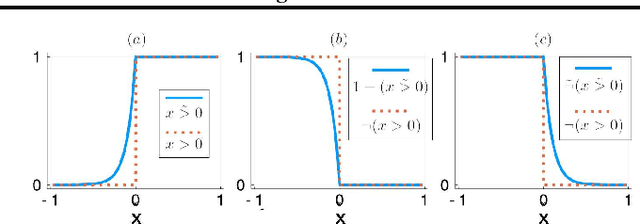
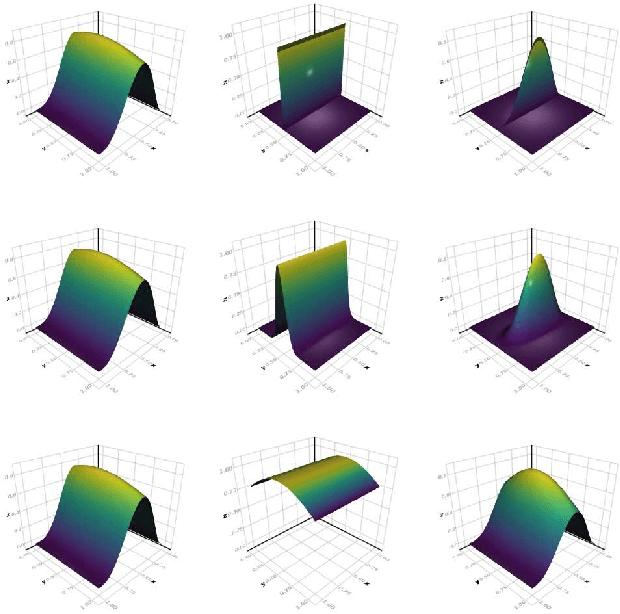
We develop a likelihood free inference procedure for conditioning a probabilistic model on a predicate. A predicate is a Boolean valued function which expresses a yes/no question about a domain. Our contribution, which we call predicate exchange, constructs a softened predicate which takes value in the unit interval [0, 1] as opposed to a simply true or false. Intuitively, 1 corresponds to true, and a high value (such as 0.999) corresponds to "nearly true" as determined by a distance metric. We define Boolean algebra for soft predicates, such that they can be negated, conjoined and disjoined arbitrarily. A softened predicate can serve as a tractable proxy to a likelihood function for approximate posterior inference. However, to target exact inference, we temper the relaxation by a temperature parameter, and add a accept/reject phase use to replica exchange Markov Chain Mont Carlo, which exchanges states between a sequence of models conditioned on predicates at varying temperatures. We describe a lightweight implementation of predicate exchange that it provides a language independent layer that can be implemented on top of existingn modeling formalisms.