NeuroAI for AI Safety

As AI systems become increasingly powerful, the need for safe AI has become more pressing. Humans are an attractive model for AI safety: as the only known agents capable of general intelligence, they perform robustly even under conditions that deviate significantly from prior experiences, explore the world safely, understand pragmatics, and can cooperate to meet their intrinsic goals. Intelligence, when coupled with cooperation and safety mechanisms, can drive sustained progress and well-being. These properties are a function of the architecture of the brain and the learning algorithms it implements. Neuroscience may thus hold important keys to technical AI safety that are currently underexplored and underutilized. In this roadmap, we highlight and critically evaluate several paths toward AI safety inspired by neuroscience: emulating the brain's representations, information processing, and architecture; building robust sensory and motor systems from imitating brain data and bodies; fine-tuning AI systems on brain data; advancing interpretability using neuroscience methods; and scaling up cognitively-inspired architectures. We make several concrete recommendations for how neuroscience can positively impact AI safety.

Automated Efficient Estimation using Monte Carlo Efficient Influence Functions

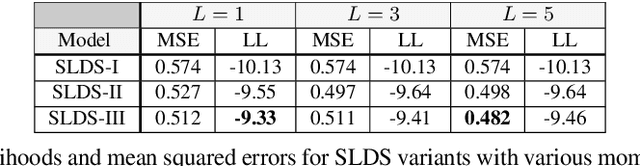
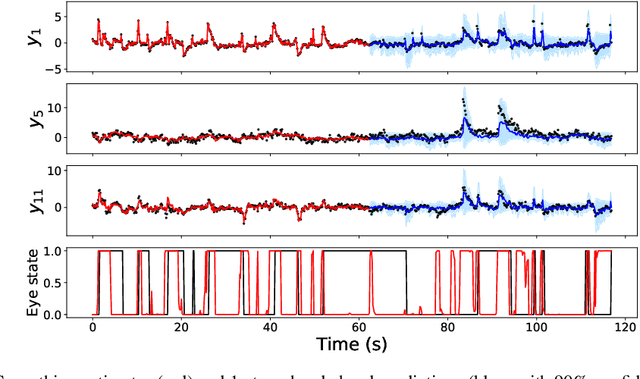
Many practical problems involve estimating low dimensional statistical quantities with high-dimensional models and datasets. Several approaches address these estimation tasks based on the theory of influence functions, such as debiased/double ML or targeted minimum loss estimation. This paper introduces \textit{Monte Carlo Efficient Influence Functions} (MC-EIF), a fully automated technique for approximating efficient influence functions that integrates seamlessly with existing differentiable probabilistic programming systems. MC-EIF automates efficient statistical estimation for a broad class of models and target functionals that would previously require rigorous custom analysis. We prove that MC-EIF is consistent, and that estimators using MC-EIF achieve optimal $\sqrt{N}$ convergence rates. We show empirically that estimators using MC-EIF are at parity with estimators using analytic EIFs. Finally, we demonstrate a novel capstone example using MC-EIF for optimal portfolio selection.

Functional Tensors for Probabilistic Programming

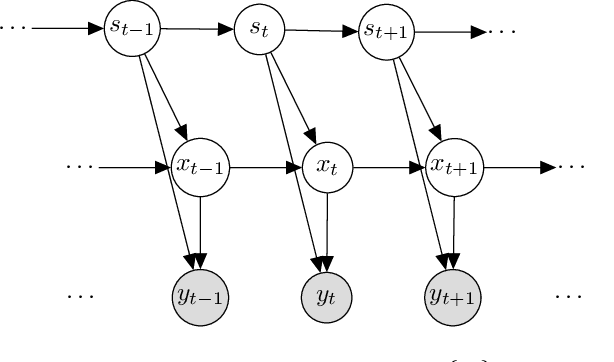
It is a significant challenge to design probabilistic programming systems that can accommodate a wide variety of inference strategies within a unified framework. Noting that the versatility of modern automatic differentiation frameworks is based in large part on the unifying concept of tensors, we describe a software abstraction --functional tensors-- that captures many of the benefits of tensors, while also being able to describe continuous probability distributions. Moreover, functional tensors are a natural candidate for generalized variable elimination and parallel-scan filtering algorithms that enable parallel exact inference for a large family of tractable modeling motifs. We demonstrate the versatility of functional tensors by integrating them into the modeling frontend and inference backend of the Pyro programming language. In experiments we show that the resulting framework enables a large variety of inference strategies, including those that mix exact and approximate inference.

Variational Estimators for Bayesian Optimal Experimental Design

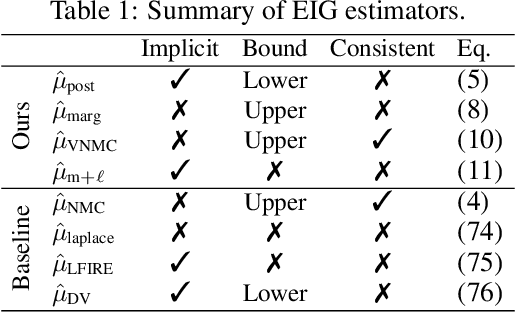
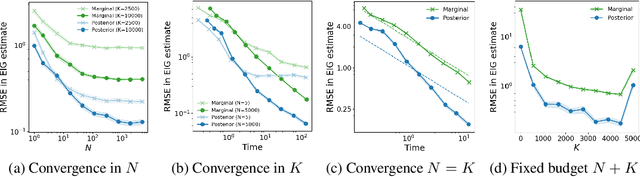
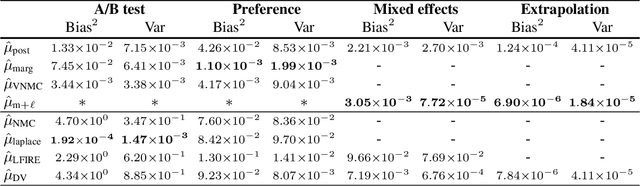
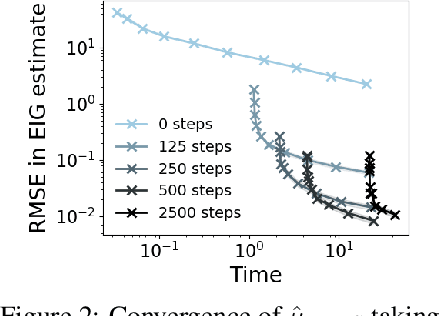
Bayesian optimal experimental design (BOED) is a principled framework for making efficient use of limited experimental resources. Unfortunately, its applicability is hampered by the difficulty of obtaining accurate estimates of the expected information gain (EIG) of an experiment. To address this, we introduce several classes of fast EIG estimators suited to the experiment design context by building on ideas from variational inference and mutual information estimation. We show theoretically and empirically that these estimators can provide significant gains in speed and accuracy over previous approaches. We demonstrate the practicality of our approach via a number of experiments, including an adaptive experiment with human participants.

Tensor Variable Elimination for Plated Factor Graphs

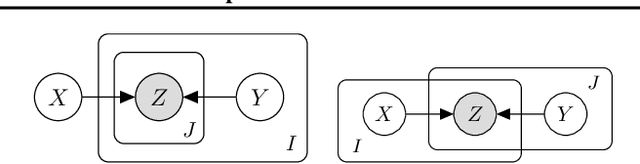
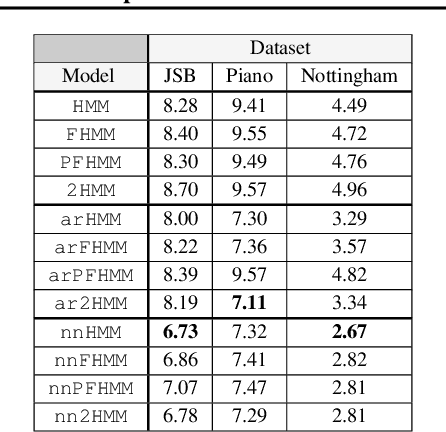
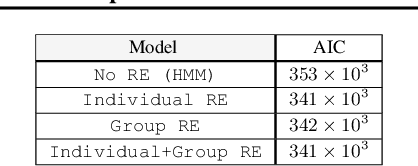
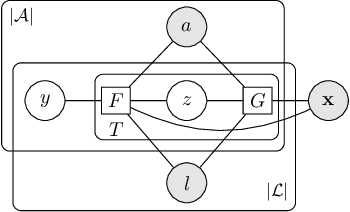
A wide class of machine learning algorithms can be reduced to variable elimination on factor graphs. While factor graphs provide a unifying notation for these algorithms, they do not provide a compact way to express repeated structure when compared to plate diagrams for directed graphical models. To exploit efficient tensor algebra in graphs with plates of variables, we generalize undirected factor graphs to plated factor graphs and variable elimination to a tensor variable elimination algorithm that operates directly on plated factor graphs. Moreover, we generalize complexity bounds based on treewidth and characterize the class of plated factor graphs for which inference is tractable. As an application, we integrate tensor variable elimination into the Pyro probabilistic programming language to enable exact inference in discrete latent variable models with repeated structure. We validate our methods with experiments on both directed and undirected graphical models, including applications to polyphonic music modeling, animal movement modeling, and latent sentiment analysis.

Pyro: Deep Universal Probabilistic Programming

Pyro is a probabilistic programming language built on Python as a platform for developing advanced probabilistic models in AI research. To scale to large datasets and high-dimensional models, Pyro uses stochastic variational inference algorithms and probability distributions built on top of PyTorch, a modern GPU-accelerated deep learning framework. To accommodate complex or model-specific algorithmic behavior, Pyro leverages Poutine, a library of composable building blocks for modifying the behavior of probabilistic programs.