Combining Induction and Transduction for Abstract Reasoning

When learning an input-output mapping from very few examples, is it better to first infer a latent function that explains the examples, or is it better to directly predict new test outputs, e.g. using a neural network? We study this question on ARC, a highly diverse dataset of abstract reasoning tasks. We train neural models for induction (inferring latent functions) and transduction (directly predicting the test output for a given test input). Our models are trained on synthetic data generated by prompting LLMs to produce Python code specifying a function to be inferred, plus a stochastic subroutine for generating inputs to that function. We find inductive and transductive models solve very different problems, despite training on the same problems, and despite sharing the same neural architecture.

Neural-guided, Bidirectional Program Search for Abstraction and Reasoning

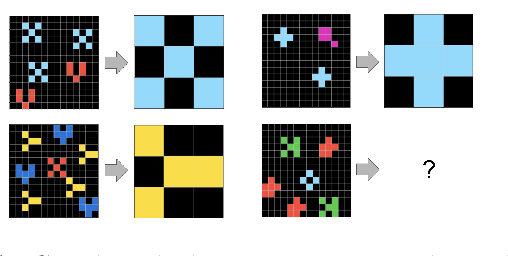
One of the challenges facing artificial intelligence research today is designing systems capable of utilizing systematic reasoning to generalize to new tasks. The Abstraction and Reasoning Corpus (ARC) measures such a capability through a set of visual reasoning tasks. In this paper we report incremental progress on ARC and lay the foundations for two approaches to abstraction and reasoning not based in brute-force search. We first apply an existing program synthesis system called DreamCoder to create symbolic abstractions out of tasks solved so far, and show how it enables solving of progressively more challenging ARC tasks. Second, we design a reasoning algorithm motivated by the way humans approach ARC. Our algorithm constructs a search graph and reasons over this graph structure to discover task solutions. More specifically, we extend existing execution-guided program synthesis approaches with deductive reasoning based on function inverse semantics to enable a neural-guided bidirectional search algorithm. We demonstrate the effectiveness of the algorithm on three domains: ARC, 24-Game tasks, and a 'double-and-add' arithmetic puzzle.

GraphChallenge.org Sparse Deep Neural Network Performance

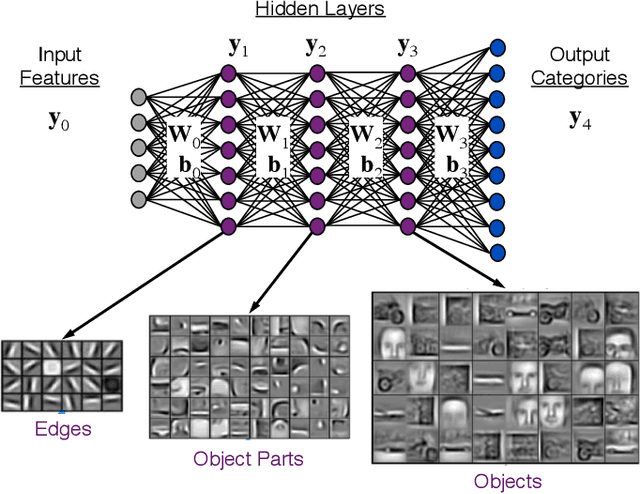
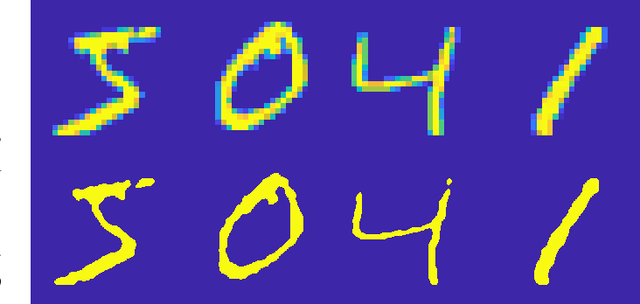
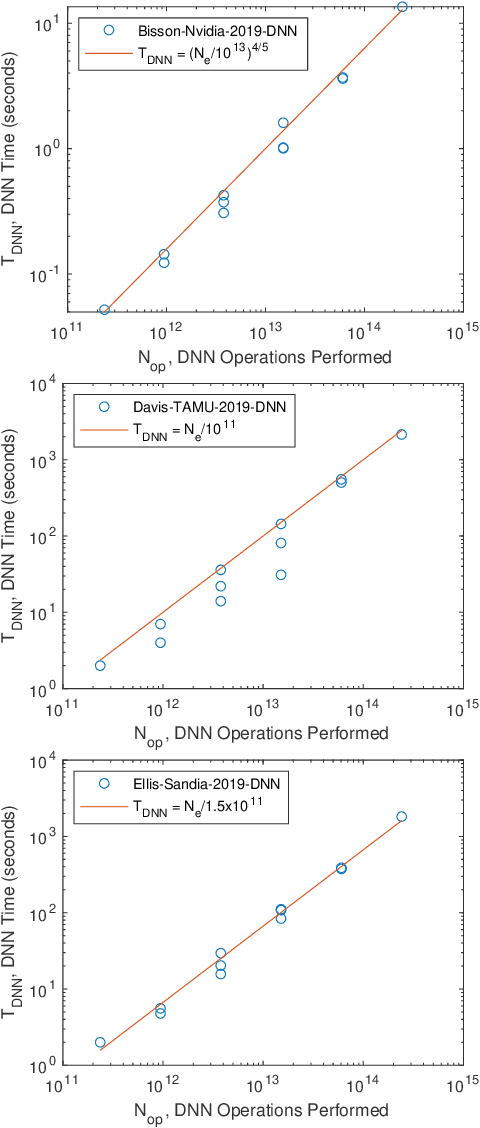
The MIT/IEEE/Amazon GraphChallenge.org encourages community approaches to developing new solutions for analyzing graphs and sparse data. Sparse AI analytics present unique scalability difficulties. The Sparse Deep Neural Network (DNN) Challenge draws upon prior challenges from machine learning, high performance computing, and visual analytics to create a challenge that is reflective of emerging sparse AI systems. The sparse DNN challenge is based on a mathematically well-defined DNN inference computation and can be implemented in any programming environment. In 2019 several sparse DNN challenge submissions were received from a wide range of authors and organizations. This paper presents a performance analysis of the best performers of these submissions. These submissions show that their state-of-the-art sparse DNN execution time, $T_{\rm DNN}$, is a strong function of the number of DNN operations performed, $N_{\rm op}$. The sparse DNN challenge provides a clear picture of current sparse DNN systems and underscores the need for new innovations to achieve high performance on very large sparse DNNs.

Sparse Deep Neural Network Graph Challenge

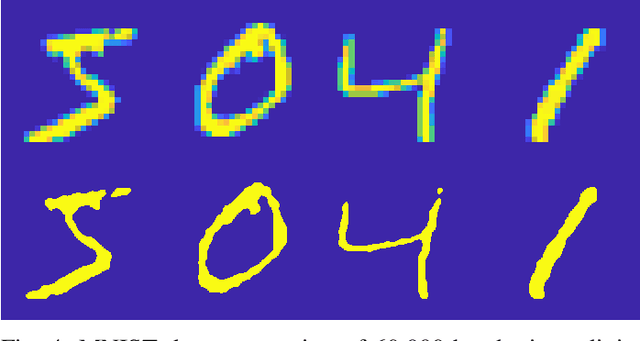
The MIT/IEEE/Amazon GraphChallenge.org encourages community approaches to developing new solutions for analyzing graphs and sparse data. Sparse AI analytics present unique scalability difficulties. The proposed Sparse Deep Neural Network (DNN) Challenge draws upon prior challenges from machine learning, high performance computing, and visual analytics to create a challenge that is reflective of emerging sparse AI systems. The Sparse DNN Challenge is based on a mathematically well-defined DNN inference computation and can be implemented in any programming environment. Sparse DNN inference is amenable to both vertex-centric implementations and array-based implementations (e.g., using the GraphBLAS.org standard). The computations are simple enough that performance predictions can be made based on simple computing hardware models. The input data sets are derived from the MNIST handwritten letters. The surrounding I/O and verification provide the context for each sparse DNN inference that allows rigorous definition of both the input and the output. Furthermore, since the proposed sparse DNN challenge is scalable in both problem size and hardware, it can be used to measure and quantitatively compare a wide range of present day and future systems. Reference implementations have been implemented and their serial and parallel performance have been measured. Specifications, data, and software are publicly available at GraphChallenge.org

Pruned and Structurally Sparse Neural Networks

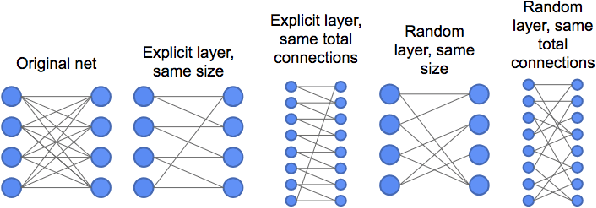
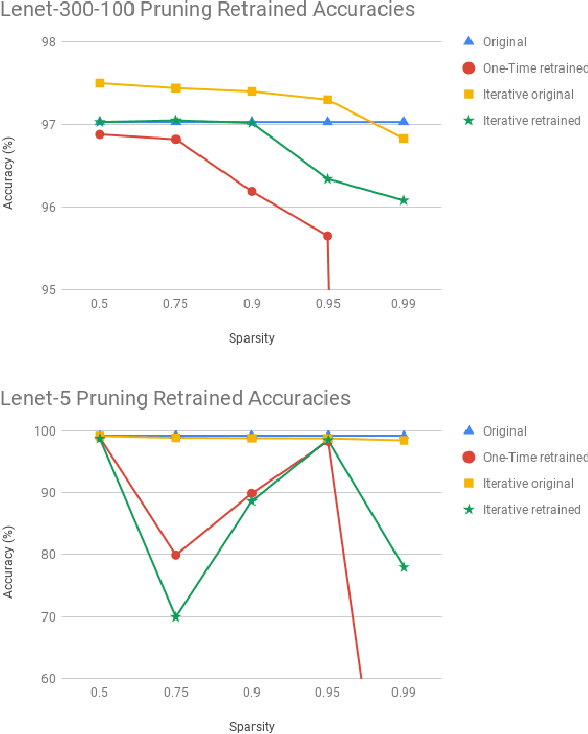
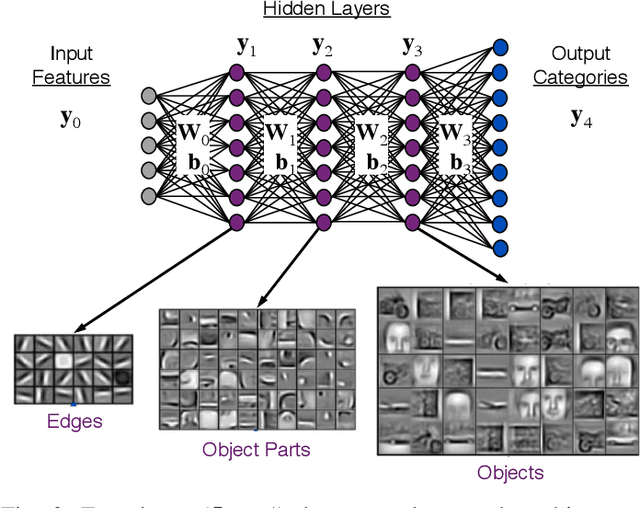
Advances in designing and training deep neural networks have led to the principle that the large and deeper a network is, the better it can perform. As a result, computational resources have become a key limiting factor in achieving better performance. One strategy to improve network capabilities while decreasing computation required is to replace dense fully-connected and convolutional layers with sparse layers. In this paper we experiment with training on sparse neural network topologies. First, we test pruning-based sparse topologies, which use a network topology obtained by initially training a dense network and then pruning low-weight connections. Second, we test RadiX-Nets, a class of sparse network structures with proven connectivity and sparsity properties. Results show that compared to dense topologies, sparse structures show promise in training potential but also can exhibit highly nonlinear convergence, which merits further study.