Sid Samsi
Maneuver Identification Challenge
Aug 25, 2021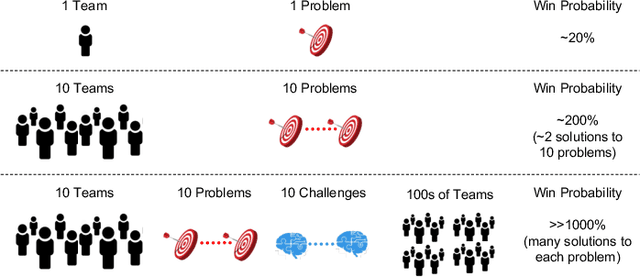
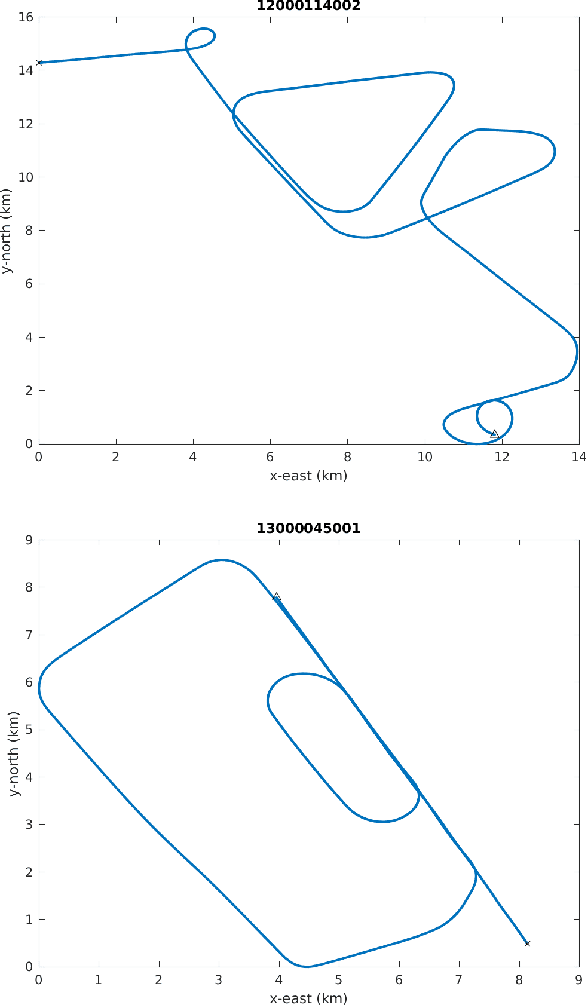
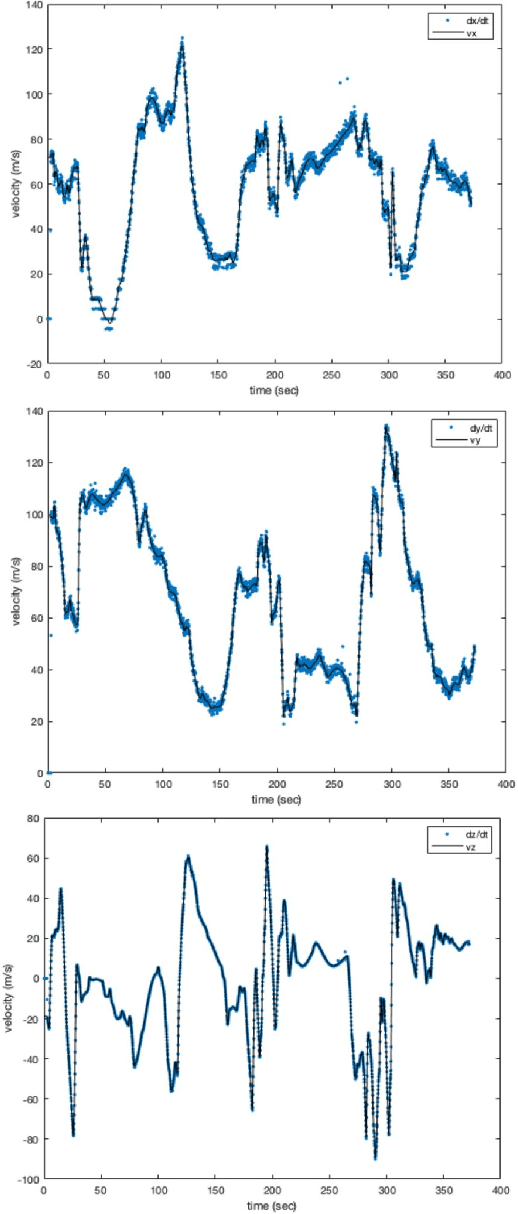

Abstract:AI algorithms that identify maneuvers from trajectory data could play an important role in improving flight safety and pilot training. AI challenges allow diverse teams to work together to solve hard problems and are an effective tool for developing AI solutions. AI challenges are also a key driver of AI computational requirements. The Maneuver Identification Challenge hosted at maneuver-id.mit.edu provides thousands of trajectories collected from pilots practicing in flight simulators, descriptions of maneuvers, and examples of these maneuvers performed by experienced pilots. Each trajectory consists of positions, velocities, and aircraft orientations normalized to a common coordinate system. Construction of the data set required significant data architecture to transform flight simulator logs into AI ready data, which included using a supercomputer for deduplication and data conditioning. There are three proposed challenges. The first challenge is separating physically plausible (good) trajectories from unfeasible (bad) trajectories. Human labeled good and bad trajectories are provided to aid in this task. Subsequent challenges are to label trajectories with their intended maneuvers and to assess the quality of those maneuvers.
GraphChallenge.org Sparse Deep Neural Network Performance
Apr 06, 2020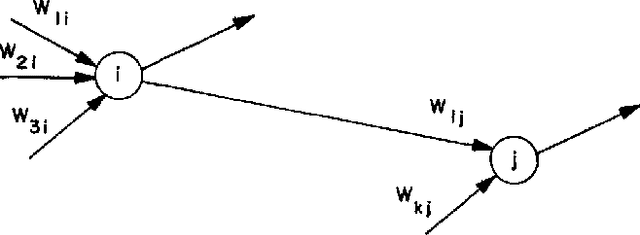
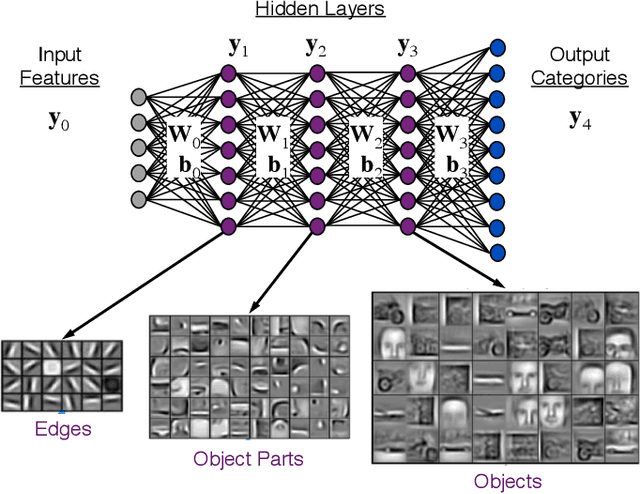
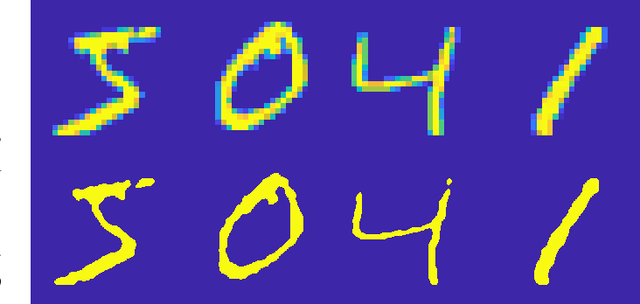
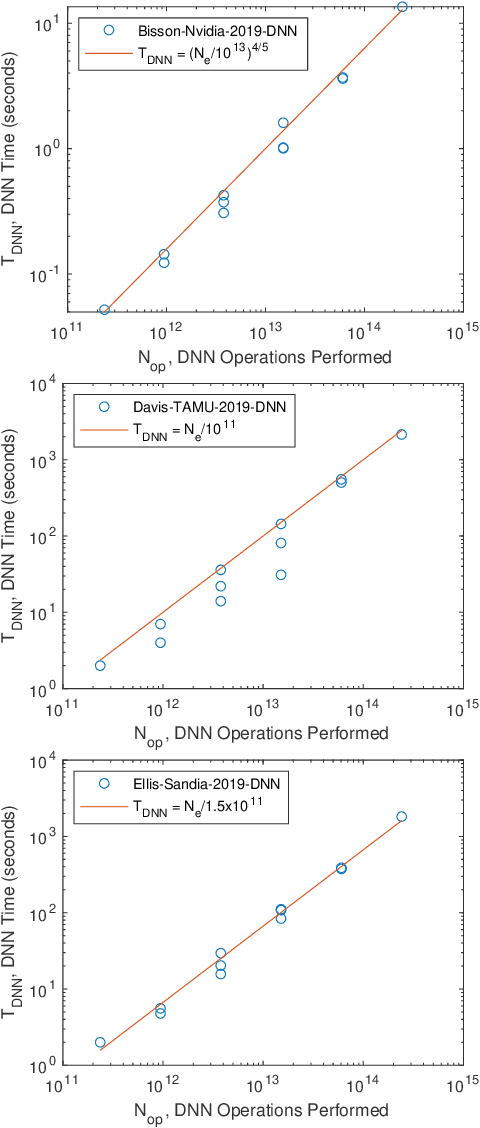
Abstract:The MIT/IEEE/Amazon GraphChallenge.org encourages community approaches to developing new solutions for analyzing graphs and sparse data. Sparse AI analytics present unique scalability difficulties. The Sparse Deep Neural Network (DNN) Challenge draws upon prior challenges from machine learning, high performance computing, and visual analytics to create a challenge that is reflective of emerging sparse AI systems. The sparse DNN challenge is based on a mathematically well-defined DNN inference computation and can be implemented in any programming environment. In 2019 several sparse DNN challenge submissions were received from a wide range of authors and organizations. This paper presents a performance analysis of the best performers of these submissions. These submissions show that their state-of-the-art sparse DNN execution time, $T_{\rm DNN}$, is a strong function of the number of DNN operations performed, $N_{\rm op}$. The sparse DNN challenge provides a clear picture of current sparse DNN systems and underscores the need for new innovations to achieve high performance on very large sparse DNNs.
Sparse Deep Neural Network Graph Challenge
Sep 02, 2019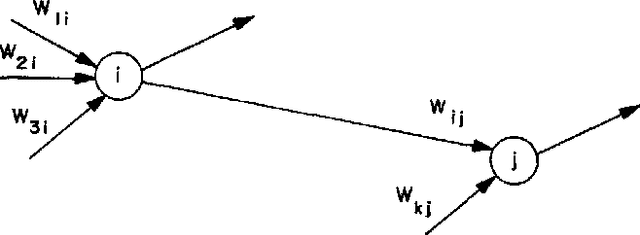
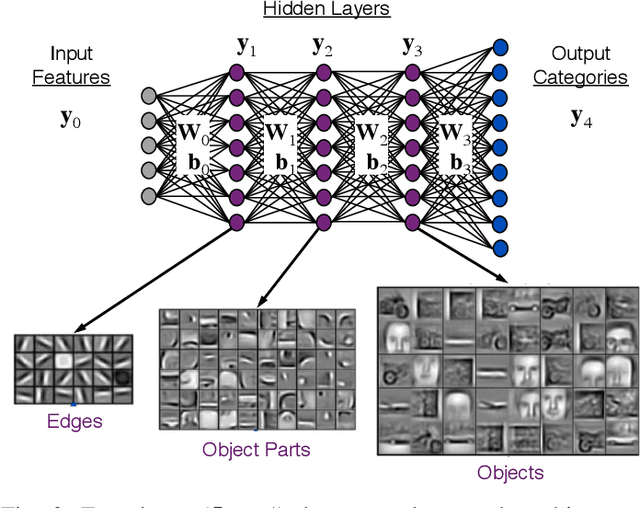
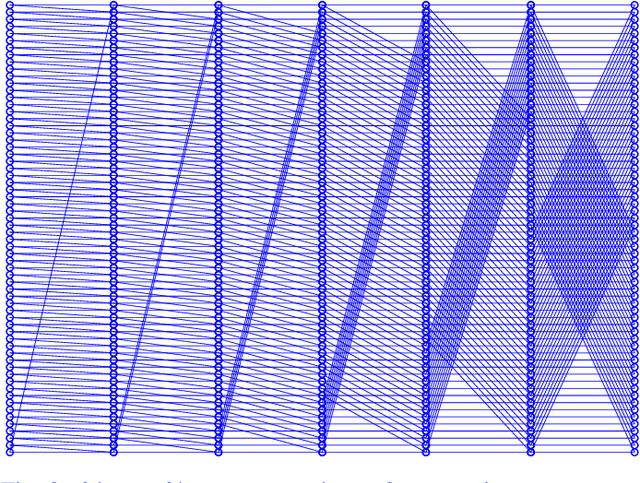
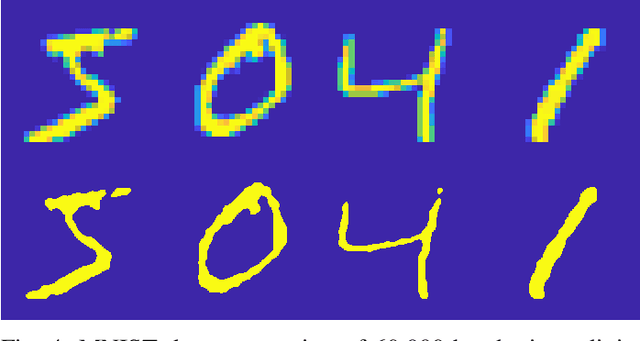
Abstract:The MIT/IEEE/Amazon GraphChallenge.org encourages community approaches to developing new solutions for analyzing graphs and sparse data. Sparse AI analytics present unique scalability difficulties. The proposed Sparse Deep Neural Network (DNN) Challenge draws upon prior challenges from machine learning, high performance computing, and visual analytics to create a challenge that is reflective of emerging sparse AI systems. The Sparse DNN Challenge is based on a mathematically well-defined DNN inference computation and can be implemented in any programming environment. Sparse DNN inference is amenable to both vertex-centric implementations and array-based implementations (e.g., using the GraphBLAS.org standard). The computations are simple enough that performance predictions can be made based on simple computing hardware models. The input data sets are derived from the MNIST handwritten letters. The surrounding I/O and verification provide the context for each sparse DNN inference that allows rigorous definition of both the input and the output. Furthermore, since the proposed sparse DNN challenge is scalable in both problem size and hardware, it can be used to measure and quantitatively compare a wide range of present day and future systems. Reference implementations have been implemented and their serial and parallel performance have been measured. Specifications, data, and software are publicly available at GraphChallenge.org
Sparse Deep Neural Network Exact Solutions
Jul 06, 2018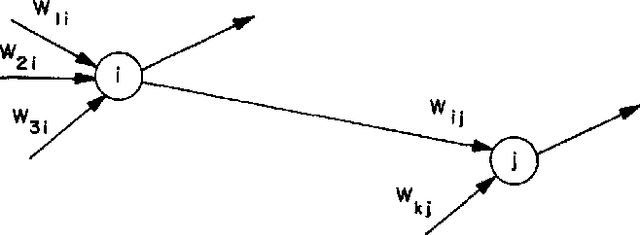
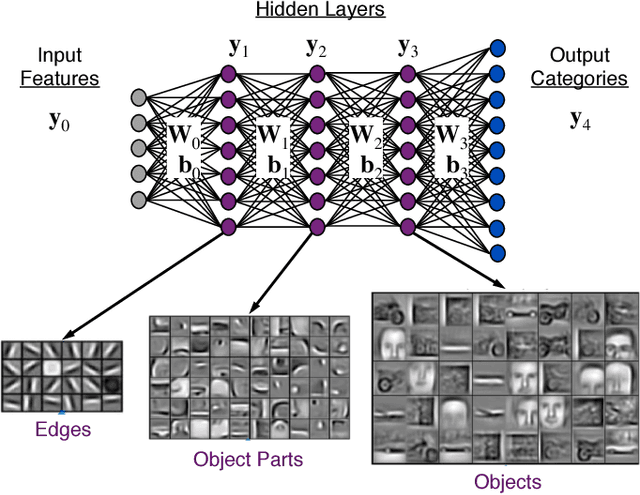
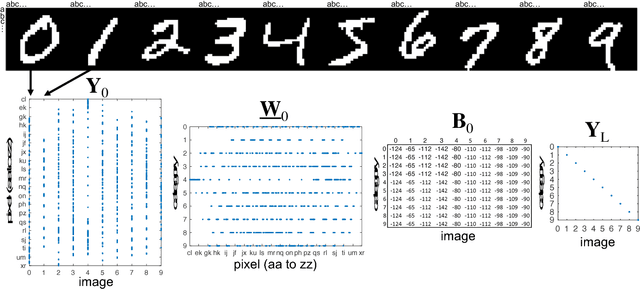
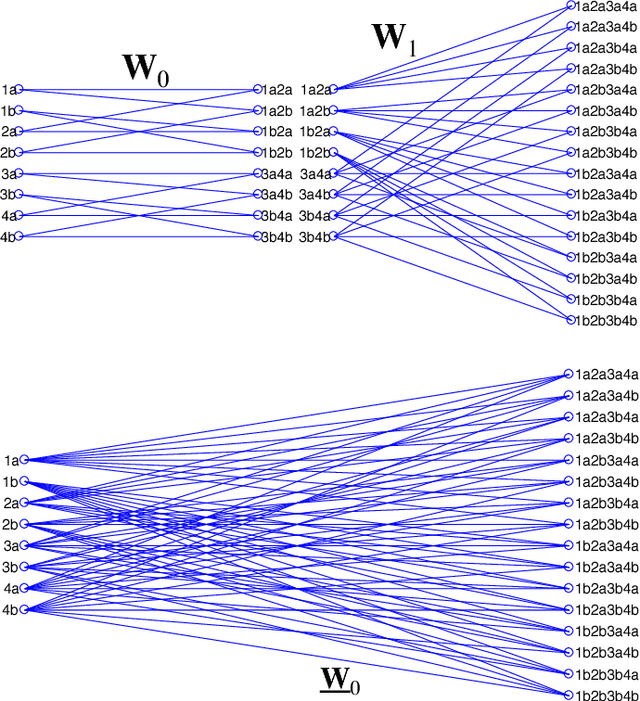
Abstract:Deep neural networks (DNNs) have emerged as key enablers of machine learning. Applying larger DNNs to more diverse applications is an important challenge. The computations performed during DNN training and inference are dominated by operations on the weight matrices describing the DNN. As DNNs incorporate more layers and more neurons per layers, these weight matrices may be required to be sparse because of memory limitations. Sparse DNNs are one possible approach, but the underlying theory is in the early stages of development and presents a number of challenges, including determining the accuracy of inference and selecting nonzero weights for training. Associative array algebra has been developed by the big data community to combine and extend database, matrix, and graph/network concepts for use in large, sparse data problems. Applying this mathematics to DNNs simplifies the formulation of DNN mathematics and reveals that DNNs are linear over oscillating semirings. This work uses associative array DNNs to construct exact solutions and corresponding perturbation models to the rectified linear unit (ReLU) DNN equations that can be used to construct test vectors for sparse DNN implementations over various precisions. These solutions can be used for DNN verification, theoretical explorations of DNN properties, and a starting point for the challenge of sparse training.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge