Complexity of One-Dimensional ReLU DNNs

We study the expressivity of one-dimensional (1D) ReLU deep neural networks through the lens of their linear regions. For randomly initialized, fully connected 1D ReLU networks (He scaling with nonzero bias) in the infinite-width limit, we prove that the expected number of linear regions grows as $\sum_{i = 1}^L n_i + \mathop{o}\left(\sum_{i = 1}^L{n_i}\right) + 1$, where $n_\ell$ denotes the number of neurons in the $\ell$-th hidden layer. We also propose a function-adaptive notion of sparsity that compares the expected regions used by the network to the minimal number needed to approximate a target within a fixed tolerance.

Accelerating AI Development with Cyber Arenas

AI development requires high fidelity testing environments to effectively transition from the laboratory to operations. The flexibility offered by cyber arenas presents a novel opportunity to test new artificial intelligence (AI) capabilities with users. Cyber arenas are designed to expose end-users to real-world situations and must rapidly incorporate evolving capabilities to meet their core objectives. To explore this concept the MIT/IEEE/Amazon Graph Challenge Anonymized Network Sensor was deployed in a cyber arena during a National Guard exercise.

Testing RadiX-Nets: Advances in Viable Sparse Topologies

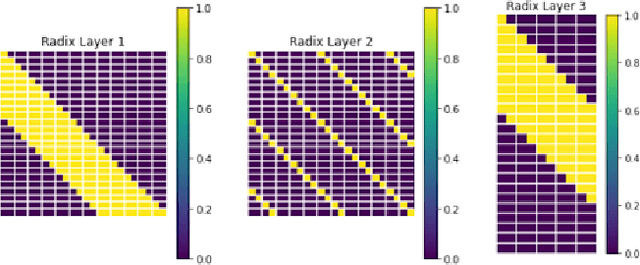
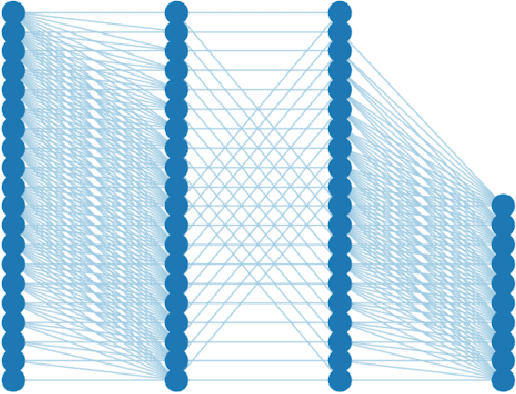
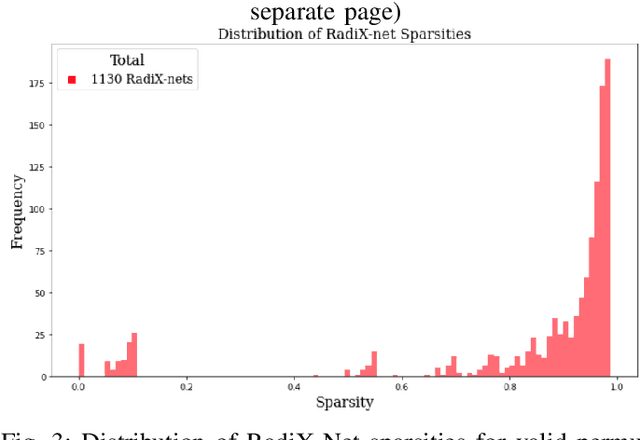
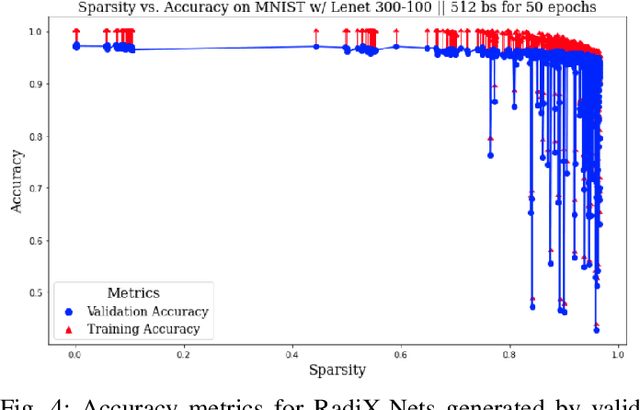
The exponential growth of data has sparked computational demands on ML research and industry use. Sparsification of hyper-parametrized deep neural networks (DNNs) creates simpler representations of complex data. Past research has shown that some sparse networks achieve similar performance as dense ones, reducing runtime and storage. RadiX-Nets, a subgroup of sparse DNNs, maintain uniformity which counteracts their lack of neural connections. Generation, independent of a dense network, yields faster asymptotic training and removes the need for costly pruning. However, little work has been done on RadiX-Nets, making testing challenging. This paper presents a testing suite for RadiX-Nets in TensorFlow. We test RadiX-Net performance to streamline processing in scalable models, revealing relationships between network topology, initialization, and training behavior. We also encounter "strange models" that train inconsistently and to lower accuracy while models of similar sparsity train well.

Complexity and Avoidance

In this dissertation we examine the relationships between the several hierarchies, including the complexity, $\mathrm{LUA}$ (Linearly Universal Avoidance), and shift complexity hierarchies, with an eye towards quantitative bounds on growth rates therein. We show that for suitable $f$ and $p$, there are $q$ and $g$ such that $\mathrm{LUA}(q) \leq_\mathrm{s} \mathrm{COMPLEX}(f)$ and $\mathrm{COMPLEX}(g) \leq_\mathrm{s} \mathrm{LUA}(p)$, as well as quantify the growth rates of $q$ and $g$. In the opposite direction, we show that for certain sub-identical $f$ satisfying $\lim_{n \to \infty}{f(n)/n}=1$ there is a $q$ such that $\mathrm{COMPLEX}(f) \leq_\mathrm{w} \mathrm{LUA}(q)$, and for certain fast-growing $p$ there is a $g$ such that $\mathrm{LUA}(p) \leq_\mathrm{s} \mathrm{COMPLEX}(g)$, as well as quantify the growth rates of $q$ and $g$. Concerning shift complexity, explicit bounds are given on how slow-growing $q$ must be for any member of $\rm{LUA}(q)$ to compute $\delta$-shift complex sequences. Motivated by the complexity hierarchy, we generalize the notion of shift complexity to consider sequences $X$ satisfying $\operatorname{KP}(\tau) \geq f(|\tau|) - O(1)$ for all substrings $\tau$ of $X$ where $f$ is any order function. We show that for sufficiently slow-growing $f$, $f$-shift complex sequences can be uniformly computed by $g$-complex sequences, where $g$ grows slightly faster than $f$. The structure of the $\mathrm{LUA}$ hierarchy is examined using bushy tree forcing, with the main result being that for any order function $p$, there is a slow-growing order function $q$ such that $\mathrm{LUA}(p)$ and $\mathrm{LUA}(q)$ are weakly incomparable. Using this, we prove new results about the filter of the weak degrees of deep nonempty $\Pi^0_1$ classes and the connection between the shift complexity and $\mathrm{LUA}$ hierarchies.

Mathematics of Digital Hyperspace

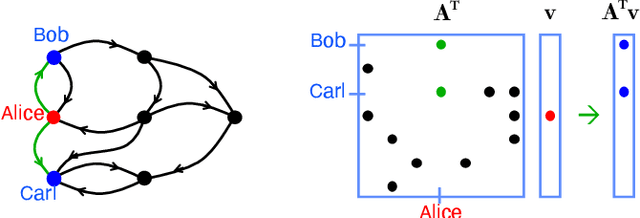
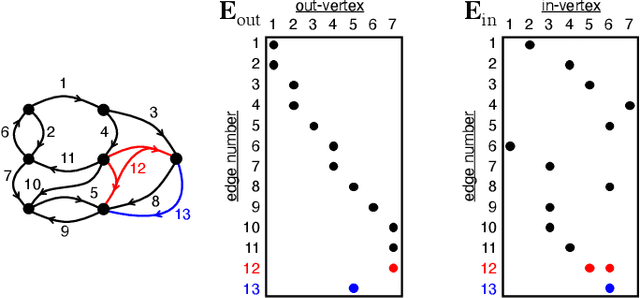
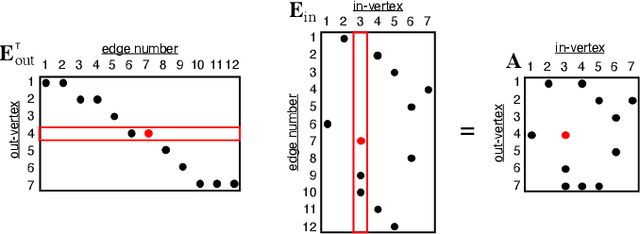
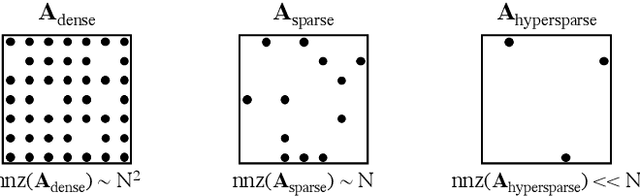
Social media, e-commerce, streaming video, e-mail, cloud documents, web pages, traffic flows, and network packets fill vast digital lakes, rivers, and oceans that we each navigate daily. This digital hyperspace is an amorphous flow of data supported by continuous streams that stretch standard concepts of type and dimension. The unstructured data of digital hyperspace can be elegantly represented, traversed, and transformed via the mathematics of hypergraphs, hypersparse matrices, and associative array algebra. This paper explores a novel mathematical concept, the semilink, that combines pairs of semirings to provide the essential operations for graph analytics, database operations, and machine learning. The GraphBLAS standard currently supports hypergraphs, hypersparse matrices, the mathematics required for semilinks, and seamlessly performs graph, network, and matrix operations. With the addition of key based indices (such as pointers to strings) and semilinks, GraphBLAS can become a richer associative array algebra and be a plug-in replacement for spreadsheets, database tables, and data centric operating systems, enhancing the navigation of unstructured data found in digital hyperspace.

Uncertainty Propagation in Deep Neural Networks Using Extended Kalman Filtering

Extended Kalman Filtering (EKF) can be used to propagate and quantify input uncertainty through a Deep Neural Network (DNN) assuming mild hypotheses on the input distribution. This methodology yields results comparable to existing methods of uncertainty propagation for DNNs while lowering the computational overhead considerably. Additionally, EKF allows model error to be naturally incorporated into the output uncertainty.

Sparse Deep Neural Network Exact Solutions

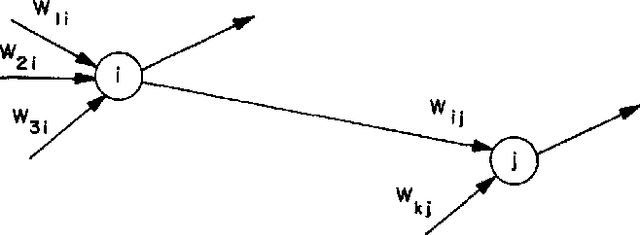
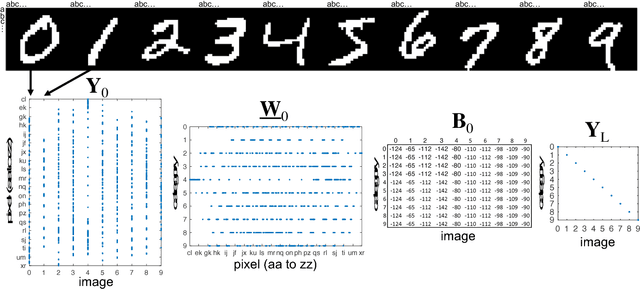
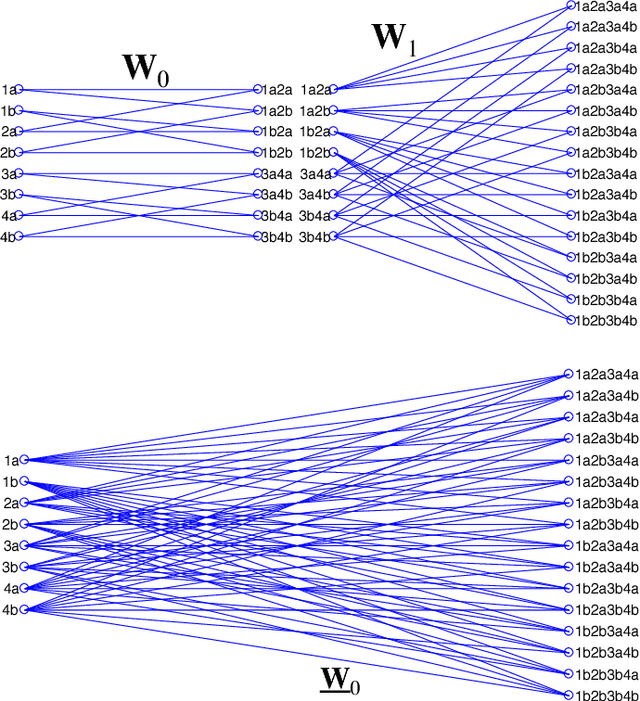
Deep neural networks (DNNs) have emerged as key enablers of machine learning. Applying larger DNNs to more diverse applications is an important challenge. The computations performed during DNN training and inference are dominated by operations on the weight matrices describing the DNN. As DNNs incorporate more layers and more neurons per layers, these weight matrices may be required to be sparse because of memory limitations. Sparse DNNs are one possible approach, but the underlying theory is in the early stages of development and presents a number of challenges, including determining the accuracy of inference and selecting nonzero weights for training. Associative array algebra has been developed by the big data community to combine and extend database, matrix, and graph/network concepts for use in large, sparse data problems. Applying this mathematics to DNNs simplifies the formulation of DNN mathematics and reveals that DNNs are linear over oscillating semirings. This work uses associative array DNNs to construct exact solutions and corresponding perturbation models to the rectified linear unit (ReLU) DNN equations that can be used to construct test vectors for sparse DNN implementations over various precisions. These solutions can be used for DNN verification, theoretical explorations of DNN properties, and a starting point for the challenge of sparse training.