Armando Solar Lezama
The Random Conditional Distribution for Higher-Order Probabilistic Inference
Mar 25, 2019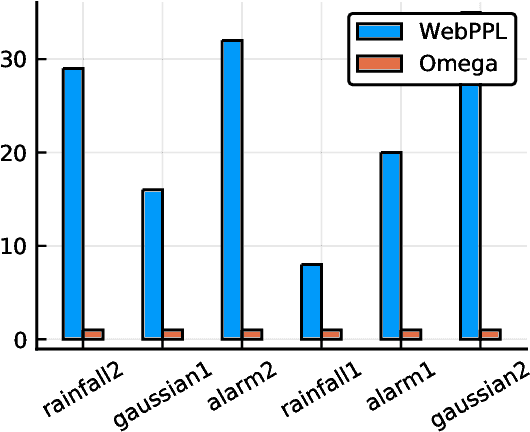


Abstract:The need to condition distributional properties such as expectation, variance, and entropy arises in algorithmic fairness, model simplification, robustness and many other areas. At face value however, distributional properties are not random variables, and hence conditioning them is a semantic error and type error in probabilistic programming languages. On the other hand, distributional properties are contingent on other variables in the model, change in value when we observe more information, and hence in a precise sense are random variables too. In order to capture the uncertain over distributional properties, we introduce a probability construct -- the random conditional distribution -- and incorporate it into a probabilistic programming language Omega. A random conditional distribution is a higher-order random variable whose realizations are themselves conditional random variables. In Omega we extend distributional properties of random variables to random conditional distributions, such that for example while the expectation a real valued random variable is a real value, the expectation of a random conditional distribution is a distribution over expectations. As a consequence, it requires minimal syntax to encode inference problems over distributional properties, which so far have evaded treatment within probabilistic programming systems and probabilistic modeling in general. We demonstrate our approach case studies in algorithmic fairness and robustness.
Soft Constraints for Inference with Declarative Knowledge
Jan 16, 2019
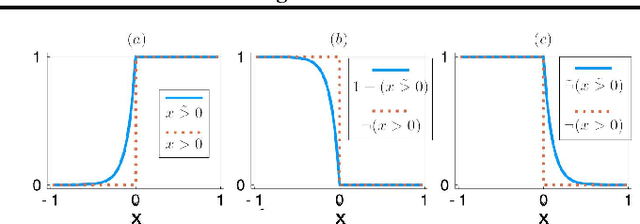
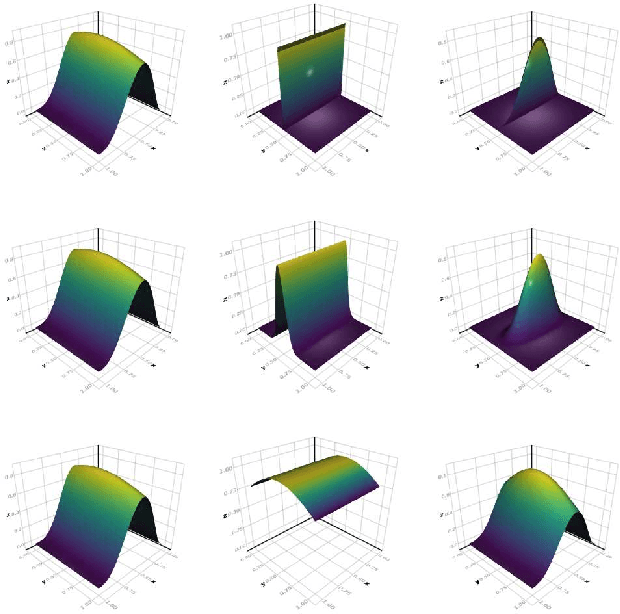
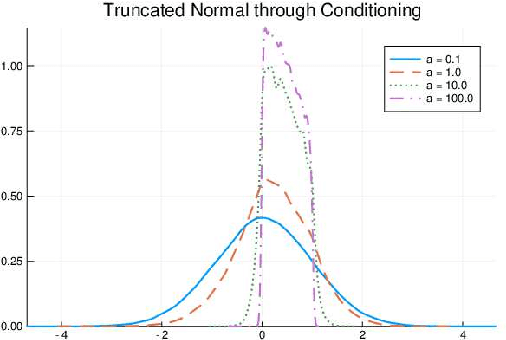
Abstract:We develop a likelihood free inference procedure for conditioning a probabilistic model on a predicate. A predicate is a Boolean valued function which expresses a yes/no question about a domain. Our contribution, which we call predicate exchange, constructs a softened predicate which takes value in the unit interval [0, 1] as opposed to a simply true or false. Intuitively, 1 corresponds to true, and a high value (such as 0.999) corresponds to "nearly true" as determined by a distance metric. We define Boolean algebra for soft predicates, such that they can be negated, conjoined and disjoined arbitrarily. A softened predicate can serve as a tractable proxy to a likelihood function for approximate posterior inference. However, to target exact inference, we temper the relaxation by a temperature parameter, and add a accept/reject phase use to replica exchange Markov Chain Mont Carlo, which exchanges states between a sequence of models conditioned on predicates at varying temperatures. We describe a lightweight implementation of predicate exchange that it provides a language independent layer that can be implemented on top of existingn modeling formalisms.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge