Random Projection Forests
Paper and Code
Oct 10, 2018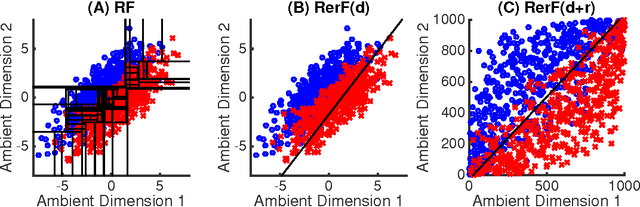
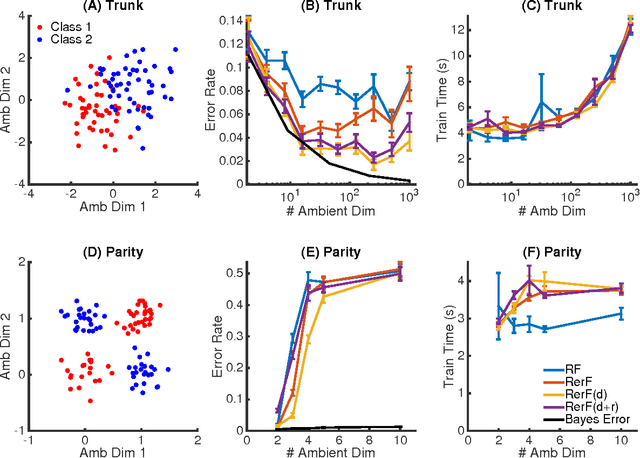
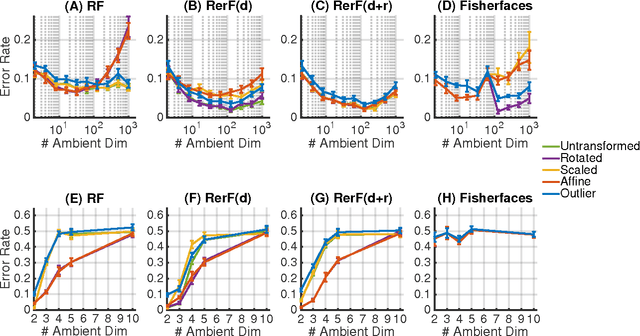
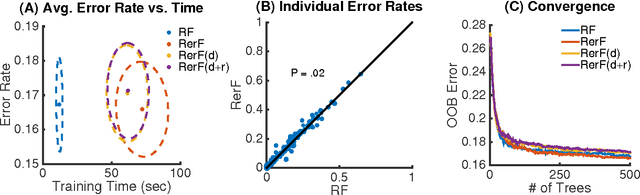
Ensemble methods---particularly those based on decision trees---have recently demonstrated superior performance in a variety of machine learning settings. We introduce a generalization of many existing decision tree methods called "Random Projection Forests" (RPF), which is any decision forest that uses (possibly data dependent and random) linear projections. Using this framework, we introduce a special case, called "Lumberjack", using very sparse random projections, that is, linear combinations of a small subset of features. Lumberjack obtains statistically significantly improved accuracy over Random Forests, Gradient Boosted Trees, and other approaches on a standard benchmark suites for classification with varying dimension, sample size, and number of classes. To illustrate how, why, and when Lumberjack outperforms other methods, we conduct extensive simulated experiments, in vectors, images, and nonlinear manifolds. Lumberjack typically yields improved performance over existing decision trees ensembles, while mitigating computational efficiency and scalability, and maintaining interpretability. Lumberjack can easily be incorporated into other ensemble methods such as boosting to obtain potentially similar gains.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge